AceParse: A Comprehensive Dataset with Diverse Structured Texts for Academic Literature Parsing

With the development of data-centric AI, the focus has shifted from model-driven approaches to improving data quality. Academic literature, as one of the crucial types, is predominantly stored in PDF formats and needs to be parsed into texts before further processing. However, parsing diverse structured texts in academic literature remains challenging due to the lack of datasets that cover various text structures. In this paper, we introduce AceParse, the first comprehensive dataset designed to support the parsing of a wide range of structured texts, including formulas, tables, lists, algorithms, and sentences with embedded mathematical expressions. Based on AceParse, we fine-tuned a multimodal model, named AceParser, which accurately parses various structured texts within academic literature. This model outperforms the previous state-of-the-art by 4.1% in terms of F1 score and by 5% in Jaccard Similarity, demonstrating the potential of multimodal models in academic literature parsing. Our dataset is available at https://github.com/JHW5981/AceParse.

Unlock the Power of Frozen LLMs in Knowledge Graph Completion

Classical knowledge graph completion (KGC) methods rely solely on structural information, struggling with the inherent sparsity of knowledge graphs (KGs). Large Language Models (LLMs) learn extensive knowledge from large corpora with powerful context modeling, which is ideal for mitigating the limitations of previous methods. Directly fine-tuning LLMs offers great capability but comes at the cost of huge time and memory consumption, while utilizing frozen LLMs yields suboptimal results. In this work, we aim to leverage LLMs for KGC effectively and efficiently. We capture the context-aware hidden states of knowledge triples by employing prompts to stimulate the intermediate layers of LLMs. We then train a data-efficient classifier on these hidden states to harness the inherent capabilities of frozen LLMs in KGC. We also generate entity descriptions with subgraph sampling on KGs, reducing the ambiguity of triplets and enriching the knowledge representation. Extensive experiments on standard benchmarks showcase the efficiency and effectiveness of our approach. We outperform classical KGC methods on most datasets and match the performance of fine-tuned LLMs. Additionally, compared to fine-tuned LLMs, we boost GPU memory efficiency by \textbf{$188\times$} and speed up training+inference by \textbf{$13.48\times$}.

Efficient Algorithms for Generalized Linear Bandits with Heavy-tailed Rewards

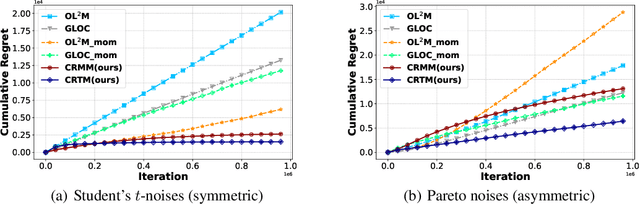
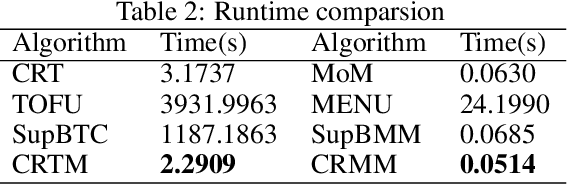
This paper investigates the problem of generalized linear bandits with heavy-tailed rewards, whose $(1+\epsilon)$-th moment is bounded for some $\epsilon\in (0,1]$. Although there exist methods for generalized linear bandits, most of them focus on bounded or sub-Gaussian rewards and are not well-suited for many real-world scenarios, such as financial markets and web-advertising. To address this issue, we propose two novel algorithms based on truncation and mean of medians. These algorithms achieve an almost optimal regret bound of $\widetilde{O}(dT^{\frac{1}{1+\epsilon}})$, where $d$ is the dimension of contextual information and $T$ is the time horizon. Our truncation-based algorithm supports online learning, distinguishing it from existing truncation-based approaches. Additionally, our mean-of-medians-based algorithm requires only $O(\log T)$ rewards and one estimator per epoch, making it more practical. Moreover, our algorithms improve the regret bounds by a logarithmic factor compared to existing algorithms when $\epsilon=1$. Numerical experimental results confirm the merits of our algorithms.

Balance Act: Mitigating Hubness in Cross-Modal Retrieval with Query and Gallery Banks

In this work, we present a post-processing solution to address the hubness problem in cross-modal retrieval, a phenomenon where a small number of gallery data points are frequently retrieved, resulting in a decline in retrieval performance. We first theoretically demonstrate the necessity of incorporating both the gallery and query data for addressing hubness as hubs always exhibit high similarity with gallery and query data. Second, building on our theoretical results, we propose a novel framework, Dual Bank Normalization (DBNorm). While previous work has attempted to alleviate hubness by only utilizing the query samples, DBNorm leverages two banks constructed from the query and gallery samples to reduce the occurrence of hubs during inference. Next, to complement DBNorm, we introduce two novel methods, dual inverted softmax and dual dynamic inverted softmax, for normalizing similarity based on the two banks. Specifically, our proposed methods reduce the similarity between hubs and queries while improving the similarity between non-hubs and queries. Finally, we present extensive experimental results on diverse language-grounded benchmarks, including text-image, text-video, and text-audio, demonstrating the superior performance of our approaches compared to previous methods in addressing hubness and boosting retrieval performance. Our code is available at https://github.com/yimuwangcs/Better_Cross_Modal_Retrieval.

Exploring and Verbalizing Academic Ideas by Concept Co-occurrence

Researchers usually come up with new ideas only after thoroughly comprehending vast quantities of literature. The difficulty of this procedure is exacerbated by the fact that the number of academic publications is growing exponentially. In this study, we devise a framework based on concept co-occurrence for academic idea inspiration, which has been integrated into a research assistant system. From our perspective, the fusion of two concepts that co-occur in an academic paper can be regarded as an important way of the emergence of a new idea. We construct evolving concept graphs according to the co-occurrence relationship of concepts from 20 disciplines or topics. Then we design a temporal link prediction method based on masked language model to explore potential connections between different concepts. To verbalize the newly discovered connections, we also utilize the pretrained language model to generate a description of an idea based on a new data structure called co-occurrence citation quintuple. We evaluate our proposed system using both automatic metrics and human assessment. The results demonstrate that our system has broad prospects and can assist researchers in expediting the process of discovering new ideas.

Nearly Optimal Regret for Stochastic Linear Bandits with Heavy-Tailed Payoffs

In this paper, we study the problem of stochastic linear bandits with finite action sets. Most of existing work assume the payoffs are bounded or sub-Gaussian, which may be violated in some scenarios such as financial markets. To settle this issue, we analyze the linear bandits with heavy-tailed payoffs, where the payoffs admit finite $1+\epsilon$ moments for some $\epsilon\in(0,1]$. Through median of means and dynamic truncation, we propose two novel algorithms which enjoy a sublinear regret bound of $\widetilde{O}(d^{\frac{1}{2}}T^{\frac{1}{1+\epsilon}})$, where $d$ is the dimension of contextual information and $T$ is the time horizon. Meanwhile, we provide an $\Omega(d^{\frac{\epsilon}{1+\epsilon}}T^{\frac{1}{1+\epsilon}})$ lower bound, which implies our upper bound matches the lower bound up to polylogarithmic factors in the order of $d$ and $T$ when $\epsilon=1$. Finally, we conduct numerical experiments to demonstrate the effectiveness of our algorithms and the empirical results strongly support our theoretical guarantees.