Exploring Polyglot Harmony: On Multilingual Data Allocation for Large Language Models Pretraining

Large language models (LLMs) have become integral to a wide range of applications worldwide, driving an unprecedented global demand for effective multilingual capabilities. Central to achieving robust multilingual performance is the strategic allocation of language proportions within training corpora. However, determining optimal language ratios is highly challenging due to intricate cross-lingual interactions and sensitivity to dataset scale. This paper introduces Climb (Cross-Lingual Interaction-aware Multilingual Balancing), a novel framework designed to systematically optimize multilingual data allocation. At its core, Climb introduces a cross-lingual interaction-aware language ratio, explicitly quantifying each language's effective allocation by capturing inter-language dependencies. Leveraging this ratio, Climb proposes a principled two-step optimization procedure--first equalizing marginal benefits across languages, then maximizing the magnitude of the resulting language allocation vectors--significantly simplifying the inherently complex multilingual optimization problem. Extensive experiments confirm that Climb can accurately measure cross-lingual interactions across various multilingual settings. LLMs trained with Climb-derived proportions consistently achieve state-of-the-art multilingual performance, even achieving competitive performance with open-sourced LLMs trained with more tokens.

TiKMiX: Take Data Influence into Dynamic Mixture for Language Model Pre-training

The data mixture used in the pre-training of a language model is a cornerstone of its final performance. However, a static mixing strategy is suboptimal, as the model's learning preferences for various data domains shift dynamically throughout training. Crucially, observing these evolving preferences in a computationally efficient manner remains a significant challenge. To address this, we propose TiKMiX, a method that dynamically adjusts the data mixture according to the model's evolving preferences. TiKMiX introduces Group Influence, an efficient metric for evaluating the impact of data domains on the model. This metric enables the formulation of the data mixing problem as a search for an optimal, influence-maximizing distribution. We solve this via two approaches: TiKMiX-D for direct optimization, and TiKMiX-M, which uses a regression model to predict a superior mixture. We trained models with different numbers of parameters, on up to 1 trillion tokens. TiKMiX-D exceeds the performance of state-of-the-art methods like REGMIX while using just 20% of the computational resources. TiKMiX-M leads to an average performance gain of 2% across 9 downstream benchmarks. Our experiments reveal that a model's data preferences evolve with training progress and scale, and we demonstrate that dynamically adjusting the data mixture based on Group Influence, a direct measure of these preferences, significantly improves performance by mitigating the underdigestion of data seen with static ratios.

MuRating: A High Quality Data Selecting Approach to Multilingual Large Language Model Pretraining

Data quality is a critical driver of large language model performance, yet existing model-based selection methods focus almost exclusively on English. We introduce MuRating, a scalable framework that transfers high-quality English data-quality signals into a single rater for 17 target languages. MuRating aggregates multiple English "raters" via pairwise comparisons to learn unified document-quality scores,then projects these judgments through translation to train a multilingual evaluator on monolingual, cross-lingual, and parallel text pairs. Applied to web data, MuRating selects balanced subsets of English and multilingual content to pretrain a 1.2 B-parameter LLaMA model. Compared to strong baselines, including QuRater, AskLLM, DCLM and so on, our approach boosts average accuracy on both English benchmarks and multilingual evaluations, with especially large gains on knowledge-intensive tasks. We further analyze translation fidelity, selection biases, and underrepresentation of narrative material, outlining directions for future work.

MuBench: Assessment of Multilingual Capabilities of Large Language Models Across 61 Languages

Multilingual large language models (LLMs) are advancing rapidly, with new models frequently claiming support for an increasing number of languages. However, existing evaluation datasets are limited and lack cross-lingual alignment, leaving assessments of multilingual capabilities fragmented in both language and skill coverage. To address this, we introduce MuBench, a benchmark covering 61 languages and evaluating a broad range of capabilities. We evaluate several state-of-the-art multilingual LLMs and find notable gaps between claimed and actual language coverage, particularly a persistent performance disparity between English and low-resource languages. Leveraging MuBench's alignment, we propose Multilingual Consistency (MLC) as a complementary metric to accuracy for analyzing performance bottlenecks and guiding model improvement. Finally, we pretrain a suite of 1.2B-parameter models on English and Chinese with 500B tokens, varying language ratios and parallel data proportions to investigate cross-lingual transfer dynamics.

MoORE: SVD-based Model MoE-ization for Conflict- and Oblivion-Resistant Multi-Task Adaptation

Adapting large-scale foundation models in multi-task scenarios often suffers from task conflict and oblivion. To mitigate such issues, we propose a novel ''model MoE-ization'' strategy that leads to a conflict- and oblivion-resistant multi-task adaptation method. Given a weight matrix of a pre-trained model, our method applies SVD to it and introduces a learnable router to adjust its singular values based on tasks and samples. Accordingly, the weight matrix becomes a Mixture of Orthogonal Rank-one Experts (MoORE), in which each expert corresponds to the outer product of a left singular vector and the corresponding right one. We can improve the model capacity by imposing a learnable orthogonal transform on the right singular vectors. Unlike low-rank adaptation (LoRA) and its MoE-driven variants, MoORE guarantees the experts' orthogonality and maintains the column space of the original weight matrix. These two properties make the adapted model resistant to the conflicts among the new tasks and the oblivion of its original tasks, respectively. Experiments on various datasets demonstrate that MoORE outperforms existing multi-task adaptation methods consistently, showing its superiority in terms of conflict- and oblivion-resistance. The code of the experiments is available at https://github.com/DaShenZi721/MoORE.

QuaDMix: Quality-Diversity Balanced Data Selection for Efficient LLM Pretraining

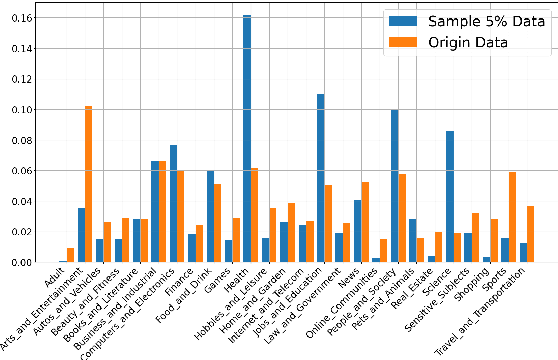
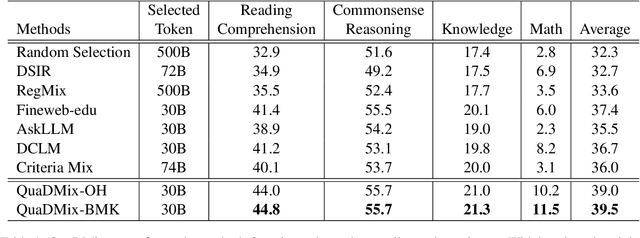
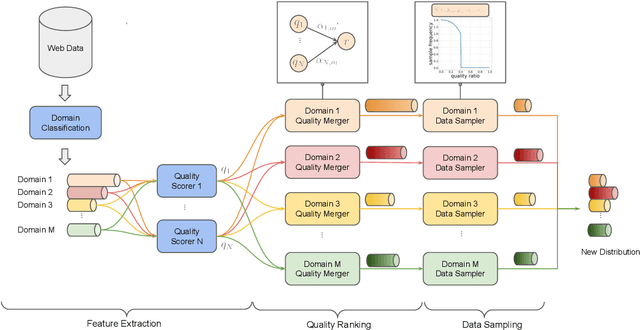
Quality and diversity are two critical metrics for the training data of large language models (LLMs), positively impacting performance. Existing studies often optimize these metrics separately, typically by first applying quality filtering and then adjusting data proportions. However, these approaches overlook the inherent trade-off between quality and diversity, necessitating their joint consideration. Given a fixed training quota, it is essential to evaluate both the quality of each data point and its complementary effect on the overall dataset. In this paper, we introduce a unified data selection framework called QuaDMix, which automatically optimizes the data distribution for LLM pretraining while balancing both quality and diversity. Specifically, we first propose multiple criteria to measure data quality and employ domain classification to distinguish data points, thereby measuring overall diversity. QuaDMix then employs a unified parameterized data sampling function that determines the sampling probability of each data point based on these quality and diversity related labels. To accelerate the search for the optimal parameters involved in the QuaDMix framework, we conduct simulated experiments on smaller models and use LightGBM for parameters searching, inspired by the RegMix method. Our experiments across diverse models and datasets demonstrate that QuaDMix achieves an average performance improvement of 7.2% across multiple benchmarks. These results outperform the independent strategies for quality and diversity, highlighting the necessity and ability to balance data quality and diversity.

Boosting 3D Adversarial Attacks with Attacking On Frequency

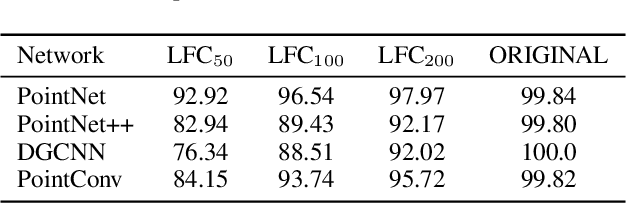
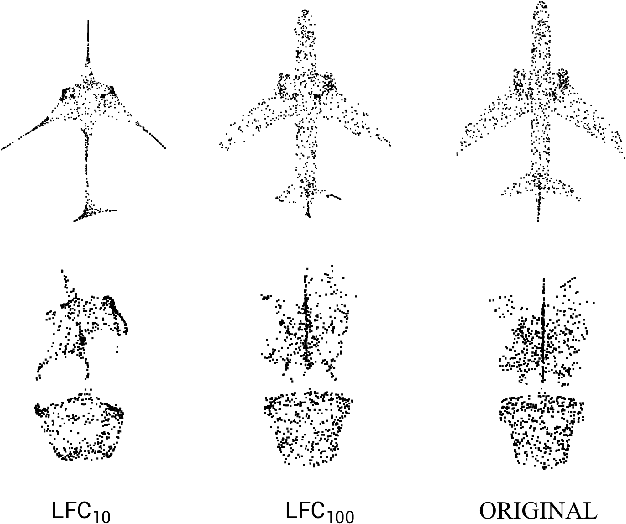
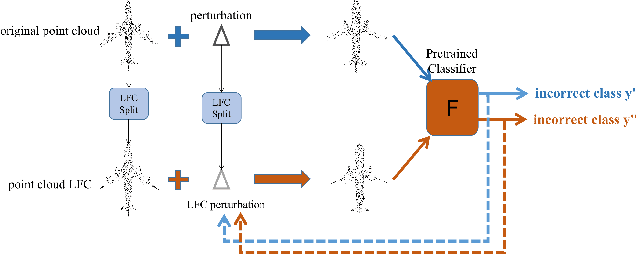
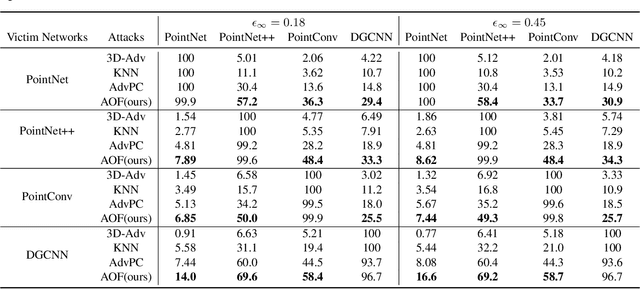
Deep neural networks (DNNs) have been shown to be vulnerable to adversarial attacks. Recently, 3D adversarial attacks, especially adversarial attacks on point clouds, have elicited mounting interest. However, adversarial point clouds obtained by previous methods show weak transferability and are easy to defend. To address these problems, in this paper we propose a novel point cloud attack (dubbed AOF) that pays more attention on the low-frequency component of point clouds. We combine the losses from point cloud and its low-frequency component to craft adversarial samples. Extensive experiments validate that AOF can improve the transferability significantly compared to state-of-the-art (SOTA) attacks, and is more robust to SOTA 3D defense methods. Otherwise, compared to clean point clouds, adversarial point clouds obtained by AOF contain more deformation than outlier.

3D Adversarial Attacks Beyond Point Cloud

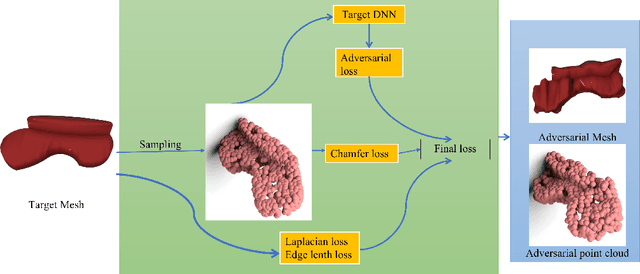
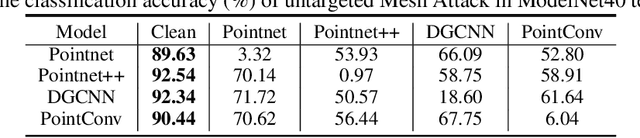
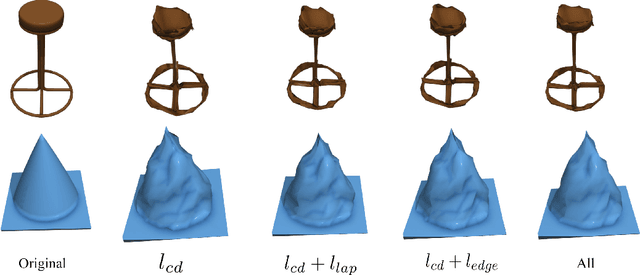
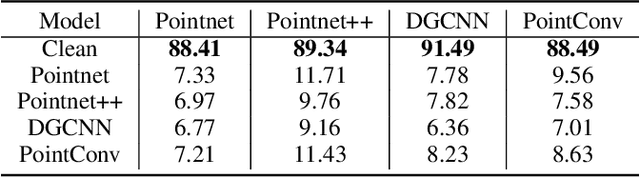
Previous adversarial attacks on 3D point clouds mainly focus on add perturbation to the original point cloud, but the generated adversarial point cloud example does not strictly represent a 3D object in the physical world and has lower transferability or easily defend by the simple SRS/SOR. In this paper, we present a novel adversarial attack, named Mesh Attack to address this problem. Specifically, we perform perturbation on the mesh instead of point clouds and obtain the adversarial mesh examples and point cloud examples simultaneously. To generate adversarial examples, we use a differential sample module that back-propagates the loss of point cloud classifier to the mesh vertices and a mesh loss that regularizes the mesh to be smooth. Extensive experiments demonstrated that the proposed scheme outperforms the SOTA attack methods. Our code is available at: {\footnotesize{\url{https://github.com/cuge1995/Mesh-Attack}}}.

The art of defense: letting networks fool the attacker

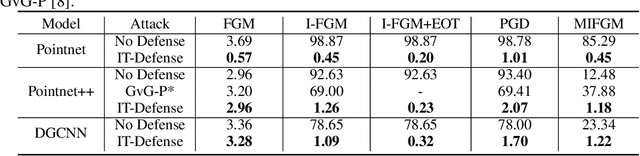
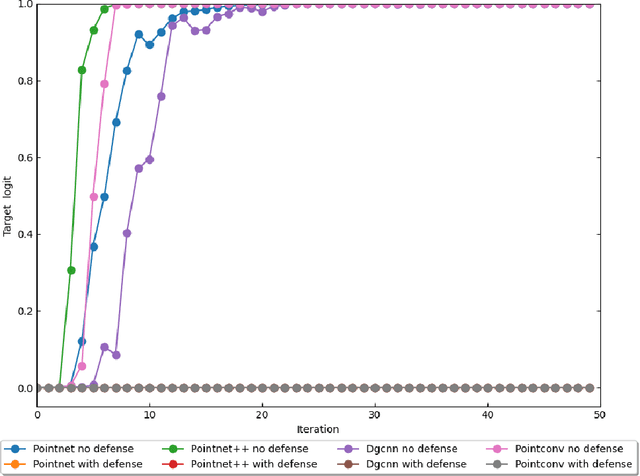
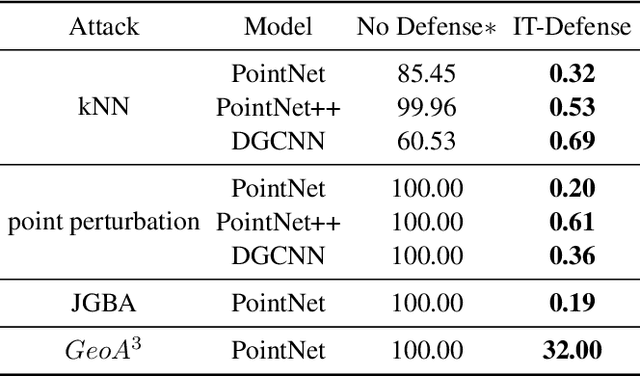
Some deep neural networks are invariant to some input transformations, such as Pointnetis permutation invariant to the input point cloud. In this paper, we demonstrated this property can be powerful in the defense of gradient based attacks. Specifically, we apply random input transformation which is invariant to networks we want to defend. Extensive experiments demonstrate that the proposed scheme outperforms the SOTA defense methods, and breaking the attack accuracy into nearly zero.

PointCutMix: Regularization Strategy for Point Cloud Classification

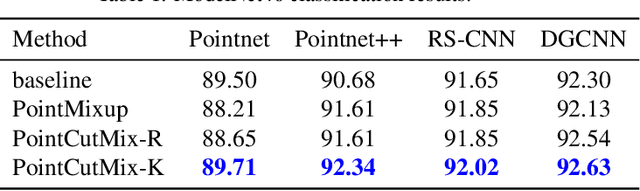
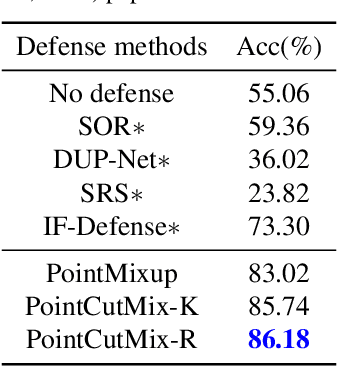
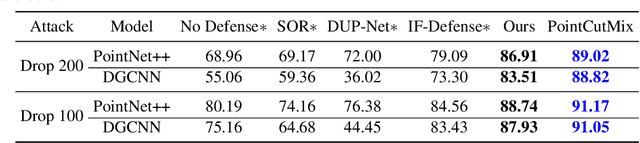
As 3D point cloud analysis has received increasing attention, the insufficient scale of point cloud datasets and the weak generalization ability of networks become prominent. In this paper, we propose a simple and effective augmentation method for the point cloud data, named PointCutMix, to alleviate those problems. It finds the optimal assignment between two point clouds and generates new training data by replacing the points in one sample with their optimal assigned pairs. Two replacement strategies are proposed to adapt to the accuracy or robustness requirement for different tasks, one of which is to randomly select all replacing points while the other one is to select k nearest neighbors of a single random point. Both strategies consistently and significantly improve the performance of various models on point cloud classification problems. By introducing the saliency maps to guide the selection of replacing points, the performance further improves. Moreover, PointCutMix is validated to enhance the model robustness against the point attack. It is worth noting that when using as a defense method, our method outperforms the state-of-the-art defense algorithms. The code is available at:https://github.com/cuge1995/PointCutMix