Offline Recommender System Evaluation under Unobserved Confounding

Off-Policy Estimation (OPE) methods allow us to learn and evaluate decision-making policies from logged data. This makes them an attractive choice for the offline evaluation of recommender systems, and several recent works have reported successful adoption of OPE methods to this end. An important assumption that makes this work is the absence of unobserved confounders: random variables that influence both actions and rewards at data collection time. Because the data collection policy is typically under the practitioner's control, the unconfoundedness assumption is often left implicit, and its violations are rarely dealt with in the existing literature. This work aims to highlight the problems that arise when performing off-policy estimation in the presence of unobserved confounders, specifically focusing on a recommendation use-case. We focus on policy-based estimators, where the logging propensities are learned from logged data. We characterise the statistical bias that arises due to confounding, and show how existing diagnostics are unable to uncover such cases. Because the bias depends directly on the true and unobserved logging propensities, it is non-identifiable. As the unconfoundedness assumption is famously untestable, this becomes especially problematic. This paper emphasises this common, yet often overlooked issue. Through synthetic data, we empirically show how na\"ive propensity estimation under confounding can lead to severely biased metric estimates that are allowed to fly under the radar. We aim to cultivate an awareness among researchers and practitioners of this important problem, and touch upon potential research directions towards mitigating its effects.

Double Clipping: Less-Biased Variance Reduction in Off-Policy Evaluation

"Clipping" (a.k.a. importance weight truncation) is a widely used variance-reduction technique for counterfactual off-policy estimators. Like other variance-reduction techniques, clipping reduces variance at the cost of increased bias. However, unlike other techniques, the bias introduced by clipping is always a downward bias (assuming non-negative rewards), yielding a lower bound on the true expected reward. In this work we propose a simple extension, called $\textit{double clipping}$, which aims to compensate this downward bias and thus reduce the overall bias, while maintaining the variance reduction properties of the original estimator.

Practical Bandits: An Industry Perspective

The bandit paradigm provides a unified modeling framework for problems that require decision-making under uncertainty. Because many business metrics can be viewed as rewards (a.k.a. utilities) that result from actions, bandit algorithms have seen a large and growing interest from industrial applications, such as search, recommendation and advertising. Indeed, with the bandit lens comes the promise of direct optimisation for the metrics we care about. Nevertheless, the road to successfully applying bandits in production is not an easy one. Even when the action space and rewards are well-defined, practitioners still need to make decisions regarding multi-arm or contextual approaches, on- or off-policy setups, delayed or immediate feedback, myopic or long-term optimisation, etc. To make matters worse, industrial platforms typically give rise to large action spaces in which existing approaches tend to break down. The research literature on these topics is broad and vast, but this can overwhelm practitioners, whose primary aim is to solve practical problems, and therefore need to decide on a specific instantiation or approach for each project. This tutorial will take a step towards filling that gap between the theory and practice of bandits. Our goal is to present a unified overview of the field and its existing terminology, concepts and algorithms -- with a focus on problems relevant to industry. We hope our industrial perspective will help future practitioners who wish to leverage the bandit paradigm for their application.

Off-policy evaluation for learning-to-rank via interpolating the item-position model and the position-based model

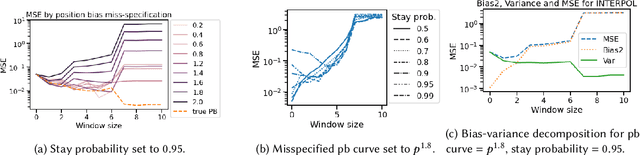
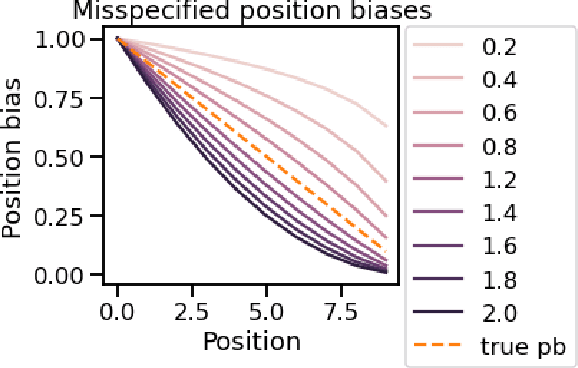
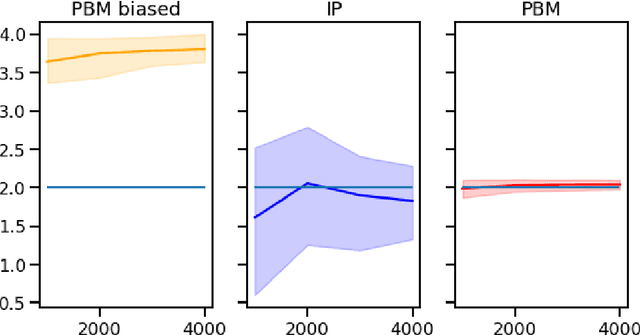
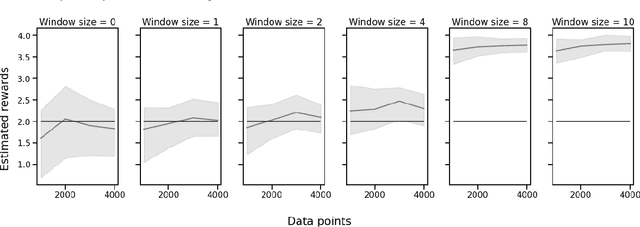
A critical need for industrial recommender systems is the ability to evaluate recommendation policies offline, before deploying them to production. Unfortunately, widely used off-policy evaluation methods either make strong assumptions about how users behave that can lead to excessive bias, or they make fewer assumptions and suffer from large variance. We tackle this problem by developing a new estimator that mitigates the problems of the two most popular off-policy estimators for rankings, namely the position-based model and the item-position model. In particular, the new estimator, called INTERPOL, addresses the bias of a potentially misspecified position-based model, while providing an adaptable bias-variance trade-off compared to the item-position model. We provide theoretical arguments as well as empirical results that highlight the performance of our novel estimation approach.

Boosted Off-Policy Learning

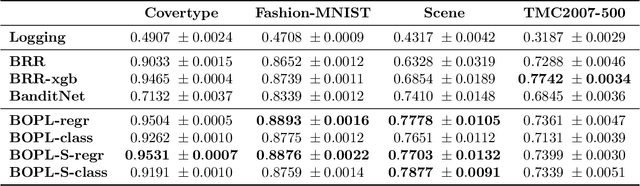
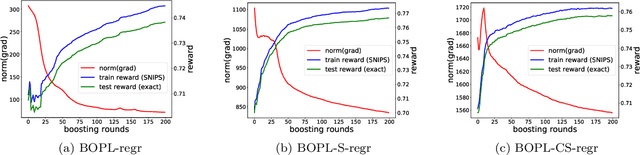
We investigate boosted ensemble models for off-policy learning from logged bandit feedback. Toward this goal, we propose a new boosting algorithm that directly optimizes an estimate of the policy's expected reward. We analyze this algorithm and prove that the empirical risk decreases (possibly exponentially fast) with each round of boosting, provided a "weak" learning condition is satisfied. We further show how the base learner reduces to standard supervised learning problems. Experiments indicate that our algorithm can outperform deep off-policy learning and methods that simply regress on the observed rewards, thereby demonstrating the benefits of both boosting and choosing the right learning objective.

Bayesian Counterfactual Risk Minimization

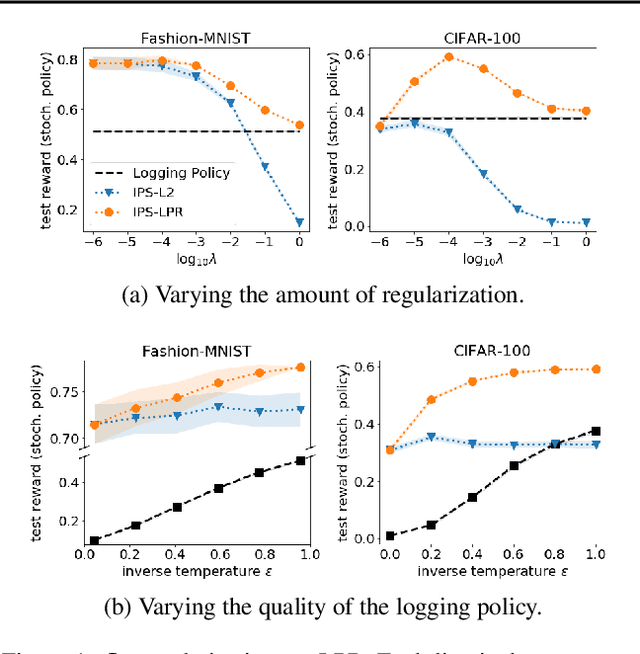
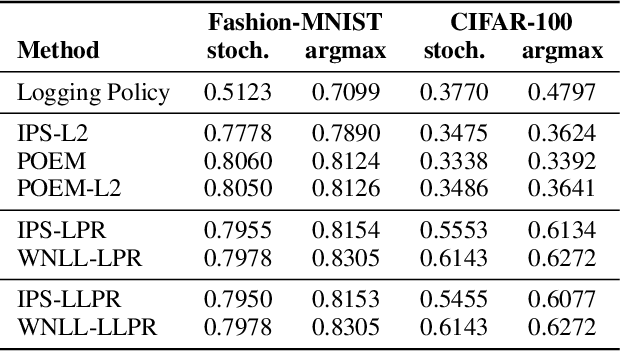
We present a Bayesian view of counterfactual risk minimization (CRM), also known as offline policy optimization from logged bandit feedback. Using PAC-Bayesian analysis, we derive a new generalization bound for the truncated IPS estimator. We apply the bound to a class of Bayesian policies, which motivates a novel, potentially data-dependent, regularization technique for CRM.

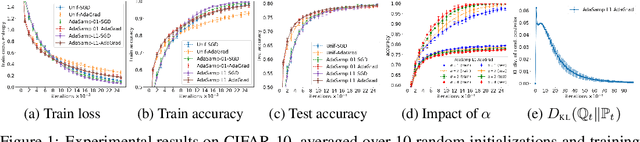
A PAC-Bayesian Analysis of Randomized Learning with Application to Stochastic Gradient Descent

We study the generalization error of randomized learning algorithms -- focusing on stochastic gradient descent (SGD) -- using a novel combination of PAC-Bayes and algorithmic stability. Importantly, our generalization bounds hold for all posterior distributions on an algorithm's random hyperparameters, including distributions that depend on the training data. This inspires an adaptive sampling algorithm for SGD that optimizes the posterior at runtime. We analyze this algorithm in the context of our generalization bounds and evaluate it on a benchmark dataset. Our experiments demonstrate that adaptive sampling can reduce empirical risk faster than uniform sampling while also improving out-of-sample accuracy.

Hinge-loss Markov Random Fields: Convex Inference for Structured Prediction

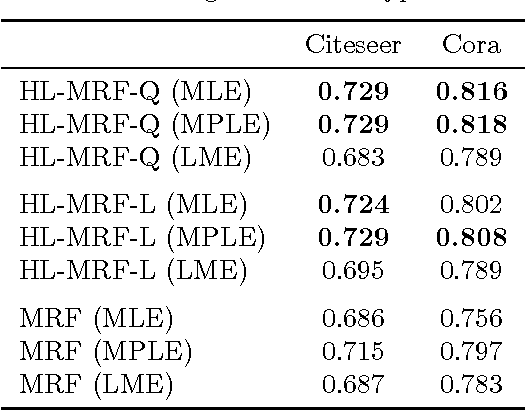
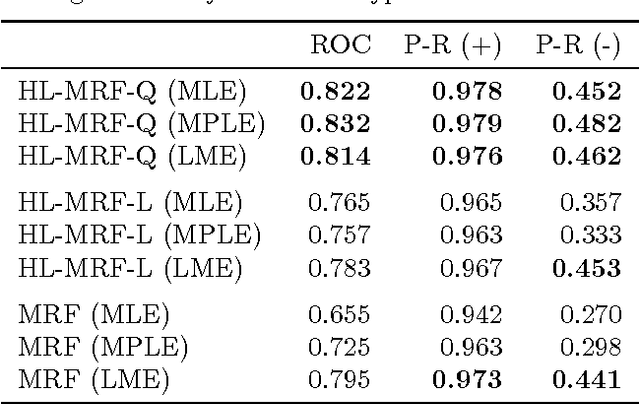
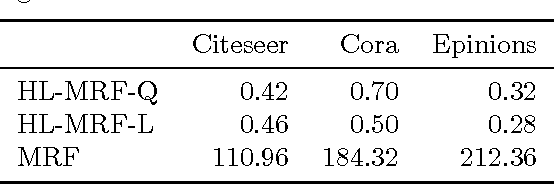
Graphical models for structured domains are powerful tools, but the computational complexities of combinatorial prediction spaces can force restrictions on models, or require approximate inference in order to be tractable. Instead of working in a combinatorial space, we use hinge-loss Markov random fields (HL-MRFs), an expressive class of graphical models with log-concave density functions over continuous variables, which can represent confidences in discrete predictions. This paper demonstrates that HL-MRFs are general tools for fast and accurate structured prediction. We introduce the first inference algorithm that is both scalable and applicable to the full class of HL-MRFs, and show how to train HL-MRFs with several learning algorithms. Our experiments show that HL-MRFs match or surpass the predictive performance of state-of-the-art methods, including discrete models, in four application domains.

Graph-based Generalization Bounds for Learning Binary Relations

We investigate the generalizability of learned binary relations: functions that map pairs of instances to a logical indicator. This problem has application in numerous areas of machine learning, such as ranking, entity resolution and link prediction. Our learning framework incorporates an example labeler that, given a sequence $X$ of $n$ instances and a desired training size $m$, subsamples $m$ pairs from $X \times X$ without replacement. The challenge in analyzing this learning scenario is that pairwise combinations of random variables are inherently dependent, which prevents us from using traditional learning-theoretic arguments. We present a unified, graph-based analysis, which allows us to analyze this dependence using well-known graph identities. We are then able to bound the generalization error of learned binary relations using Rademacher complexity and algorithmic stability. The rate of uniform convergence is partially determined by the labeler's subsampling process. We thus examine how various assumptions about subsampling affect generalization; under a natural random subsampling process, our bounds guarantee $\tilde{O}(1/\sqrt{n})$ uniform convergence.

Multi-relational Learning Using Weighted Tensor Decomposition with Modular Loss

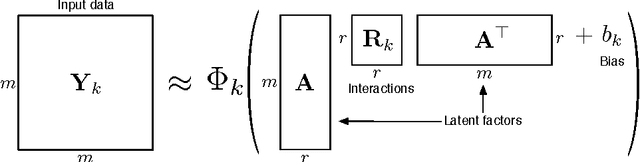
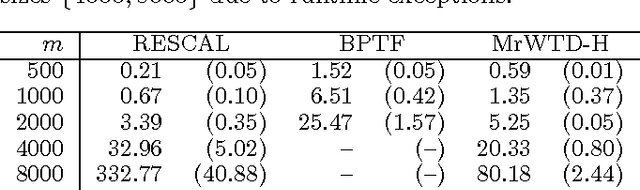
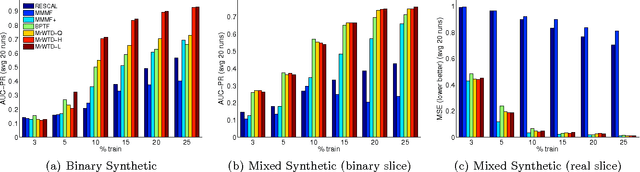
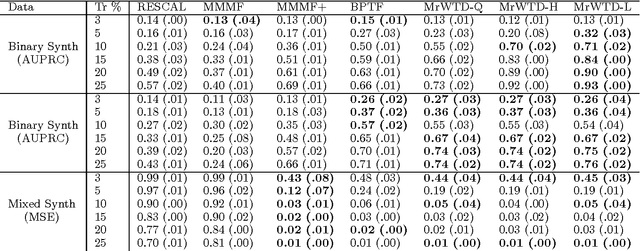
We propose a modular framework for multi-relational learning via tensor decomposition. In our learning setting, the training data contains multiple types of relationships among a set of objects, which we represent by a sparse three-mode tensor. The goal is to predict the values of the missing entries. To do so, we model each relationship as a function of a linear combination of latent factors. We learn this latent representation by computing a low-rank tensor decomposition, using quasi-Newton optimization of a weighted objective function. Sparsity in the observed data is captured by the weighted objective, leading to improved accuracy when training data is limited. Exploiting sparsity also improves efficiency, potentially up to an order of magnitude over unweighted approaches. In addition, our framework accommodates arbitrary combinations of smooth, task-specific loss functions, making it better suited for learning different types of relations. For the typical cases of real-valued functions and binary relations, we propose several loss functions and derive the associated parameter gradients. We evaluate our method on synthetic and real data, showing significant improvements in both accuracy and scalability over related factorization techniques.