Bayesian Counterfactual Risk Minimization
Paper and Code
Oct 30, 2018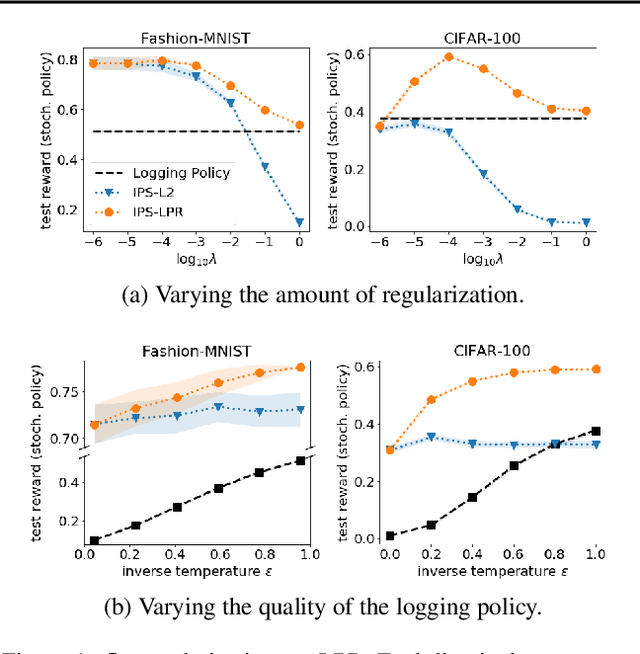
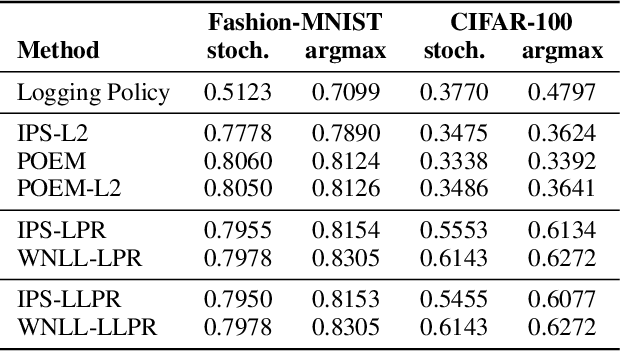
We present a Bayesian view of counterfactual risk minimization (CRM), also known as offline policy optimization from logged bandit feedback. Using PAC-Bayesian analysis, we derive a new generalization bound for the truncated IPS estimator. We apply the bound to a class of Bayesian policies, which motivates a novel, potentially data-dependent, regularization technique for CRM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge