Multi-relational Learning Using Weighted Tensor Decomposition with Modular Loss
Paper and Code
May 31, 2013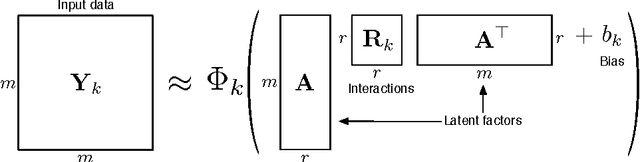
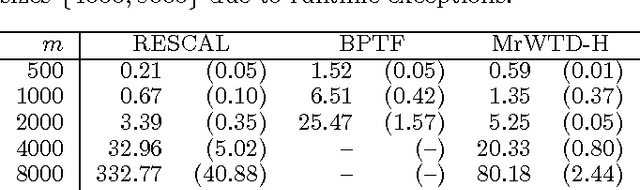
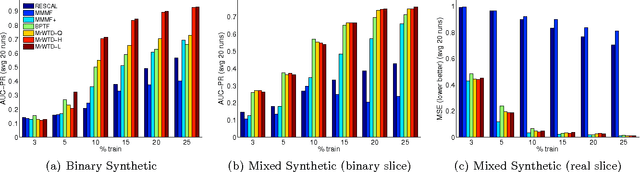
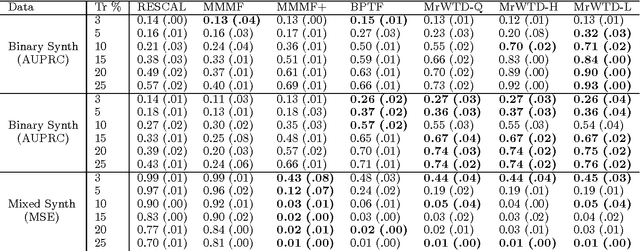
We propose a modular framework for multi-relational learning via tensor decomposition. In our learning setting, the training data contains multiple types of relationships among a set of objects, which we represent by a sparse three-mode tensor. The goal is to predict the values of the missing entries. To do so, we model each relationship as a function of a linear combination of latent factors. We learn this latent representation by computing a low-rank tensor decomposition, using quasi-Newton optimization of a weighted objective function. Sparsity in the observed data is captured by the weighted objective, leading to improved accuracy when training data is limited. Exploiting sparsity also improves efficiency, potentially up to an order of magnitude over unweighted approaches. In addition, our framework accommodates arbitrary combinations of smooth, task-specific loss functions, making it better suited for learning different types of relations. For the typical cases of real-valued functions and binary relations, we propose several loss functions and derive the associated parameter gradients. We evaluate our method on synthetic and real data, showing significant improvements in both accuracy and scalability over related factorization techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge