Babak Esmaeili
SAFE--MA--RRT: Multi-Agent Motion Planning with Data-Driven Safety Certificates
Sep 04, 2025Abstract:This paper proposes a fully data-driven motion-planning framework for homogeneous linear multi-agent systems that operate in shared, obstacle-filled workspaces without access to explicit system models. Each agent independently learns its closed-loop behavior from experimental data by solving convex semidefinite programs that generate locally invariant ellipsoids and corresponding state-feedback gains. These ellipsoids, centered along grid-based waypoints, certify the dynamic feasibility of short-range transitions and define safe regions of operation. A sampling-based planner constructs a tree of such waypoints, where transitions are allowed only when adjacent ellipsoids overlap, ensuring invariant-to-invariant transitions and continuous safety. All agents expand their trees simultaneously and are coordinated through a space-time reservation table that guarantees inter-agent safety by preventing simultaneous occupancy and head-on collisions. Each successful edge in the tree is equipped with its own local controller, enabling execution without re-solving optimization problems at runtime. The resulting trajectories are not only dynamically feasible but also provably safe with respect to both environmental constraints and inter-agent collisions. Simulation results demonstrate the effectiveness of the approach in synthesizing synchronized, safe trajectories for multiple agents under shared dynamics and constraints, using only data and convex optimization tools.
Data-Driven Motion Planning for Uncertain Nonlinear Systems
Jul 31, 2025Abstract:This paper proposes a data-driven motion-planning framework for nonlinear systems that constructs a sequence of overlapping invariant polytopes. Around each randomly sampled waypoint, the algorithm identifies a convex admissible region and solves data-driven linear-matrix-inequality problems to learn several ellipsoidal invariant sets together with their local state-feedback gains. The convex hull of these ellipsoids, still invariant under a piece-wise-affine controller obtained by interpolating the gains, is then approximated by a polytope. Safe transitions between nodes are ensured by verifying the intersection of consecutive convex-hull polytopes and introducing an intermediate node for a smooth transition. Control gains are interpolated in real time via simplex-based interpolation, keeping the state inside the invariant polytopes throughout the motion. Unlike traditional approaches that rely on system dynamics models, our method requires only data to compute safe regions and design state-feedback controllers. The approach is validated through simulations, demonstrating the effectiveness of the proposed method in achieving safe, dynamically feasible paths for complex nonlinear systems.
Risk-Aware Safe Reinforcement Learning for Control of Stochastic Linear Systems
May 14, 2025Abstract:This paper presents a risk-aware safe reinforcement learning (RL) control design for stochastic discrete-time linear systems. Rather than using a safety certifier to myopically intervene with the RL controller, a risk-informed safe controller is also learned besides the RL controller, and the RL and safe controllers are combined together. Several advantages come along with this approach: 1) High-confidence safety can be certified without relying on a high-fidelity system model and using limited data available, 2) Myopic interventions and convergence to an undesired equilibrium can be avoided by deciding on the contribution of two stabilizing controllers, and 3) highly efficient and computationally tractable solutions can be provided by optimizing over a scalar decision variable and linear programming polyhedral sets. To learn safe controllers with a large invariant set, piecewise affine controllers are learned instead of linear controllers. To this end, the closed-loop system is first represented using collected data, a decision variable, and noise. The effect of the decision variable on the variance of the safe violation of the closed-loop system is formalized. The decision variable is then designed such that the probability of safety violation for the learned closed-loop system is minimized. It is shown that this control-oriented approach reduces the data requirements and can also reduce the variance of safety violations. Finally, to integrate the safe and RL controllers, a new data-driven interpolation technique is introduced. This method aims to maintain the RL agent's optimal implementation while ensuring its safety within environments characterized by noise. The study concludes with a simulation example that serves to validate the theoretical results.
Variational Stochastic Gradient Descent for Deep Neural Networks
Apr 09, 2024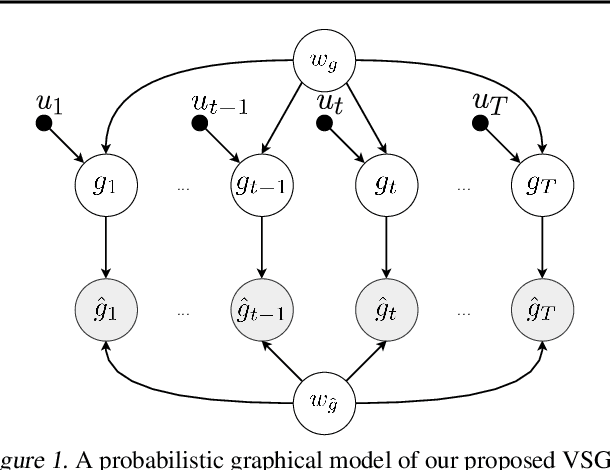
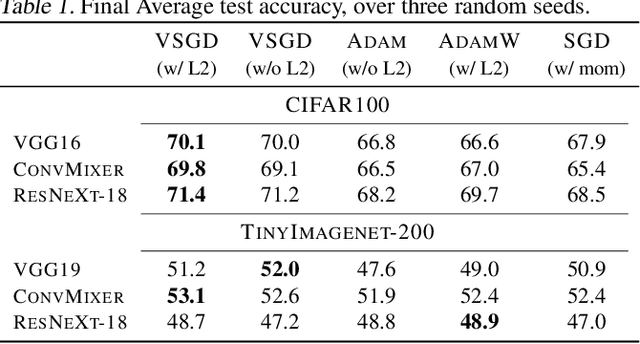
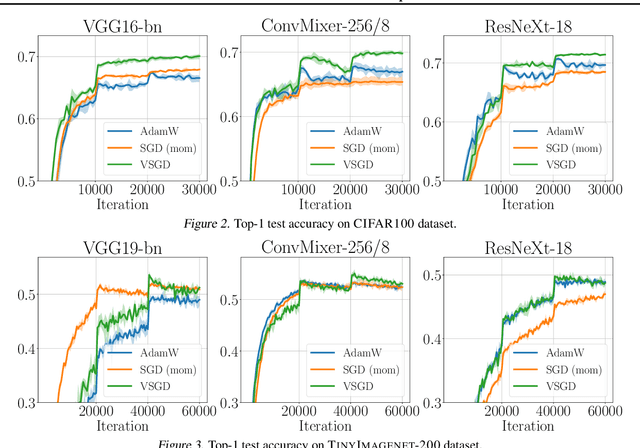
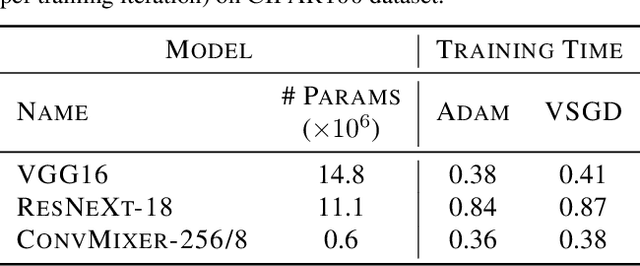
Abstract:Optimizing deep neural networks is one of the main tasks in successful deep learning. Current state-of-the-art optimizers are adaptive gradient-based optimization methods such as Adam. Recently, there has been an increasing interest in formulating gradient-based optimizers in a probabilistic framework for better estimation of gradients and modeling uncertainties. Here, we propose to combine both approaches, resulting in the Variational Stochastic Gradient Descent (VSGD) optimizer. We model gradient updates as a probabilistic model and utilize stochastic variational inference (SVI) to derive an efficient and effective update rule. Further, we show how our VSGD method relates to other adaptive gradient-based optimizers like Adam. Lastly, we carry out experiments on two image classification datasets and four deep neural network architectures, where we show that VSGD outperforms Adam and SGD.
Topological Obstructions and How to Avoid Them
Dec 12, 2023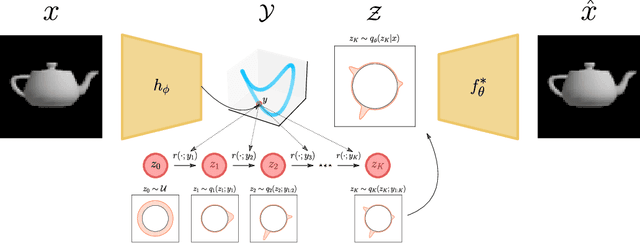
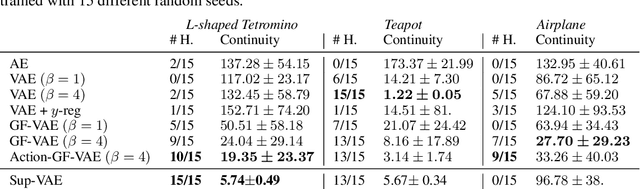


Abstract:Incorporating geometric inductive biases into models can aid interpretability and generalization, but encoding to a specific geometric structure can be challenging due to the imposed topological constraints. In this paper, we theoretically and empirically characterize obstructions to training encoders with geometric latent spaces. We show that local optima can arise due to singularities (e.g. self-intersection) or due to an incorrect degree or winding number. We then discuss how normalizing flows can potentially circumvent these obstructions by defining multimodal variational distributions. Inspired by this observation, we propose a new flow-based model that maps data points to multimodal distributions over geometric spaces and empirically evaluate our model on 2 domains. We observe improved stability during training and a higher chance of converging to a homeomorphic encoder.
Conjugate Energy-Based Models
Jun 25, 2021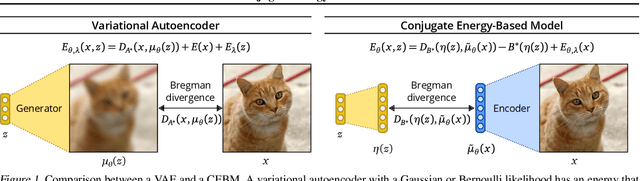
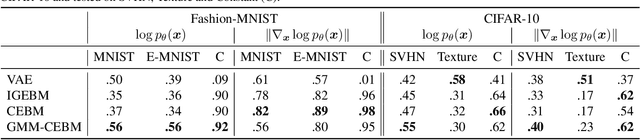

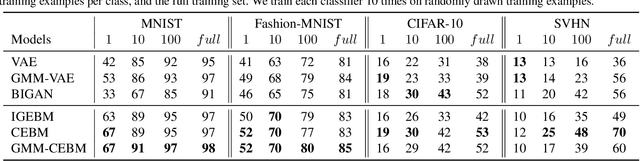
Abstract:In this paper, we propose conjugate energy-based models (CEBMs), a new class of energy-based models that define a joint density over data and latent variables. The joint density of a CEBM decomposes into an intractable distribution over data and a tractable posterior over latent variables. CEBMs have similar use cases as variational autoencoders, in the sense that they learn an unsupervised mapping from data to latent variables. However, these models omit a generator network, which allows them to learn more flexible notions of similarity between data points. Our experiments demonstrate that conjugate EBMs achieve competitive results in terms of image modelling, predictive power of latent space, and out-of-domain detection on a variety of datasets.
Nested Variational Inference
Jun 21, 2021

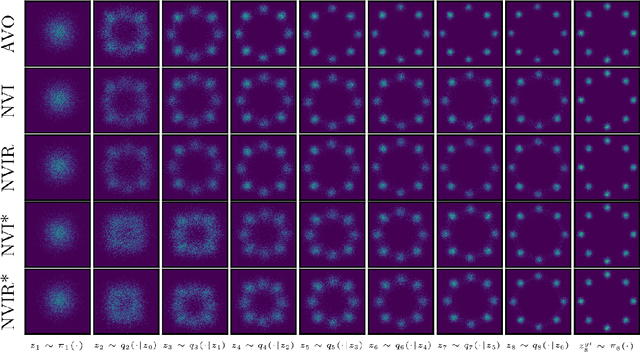

Abstract:We develop nested variational inference (NVI), a family of methods that learn proposals for nested importance samplers by minimizing an forward or reverse KL divergence at each level of nesting. NVI is applicable to many commonly-used importance sampling strategies and provides a mechanism for learning intermediate densities, which can serve as heuristics to guide the sampler. Our experiments apply NVI to (a) sample from a multimodal distribution using a learned annealing path (b) learn heuristics that approximate the likelihood of future observations in a hidden Markov model and (c) to perform amortized inference in hierarchical deep generative models. We observe that optimizing nested objectives leads to improved sample quality in terms of log average weight and effective sample size.
Evaluating Combinatorial Generalization in Variational Autoencoders
Nov 11, 2019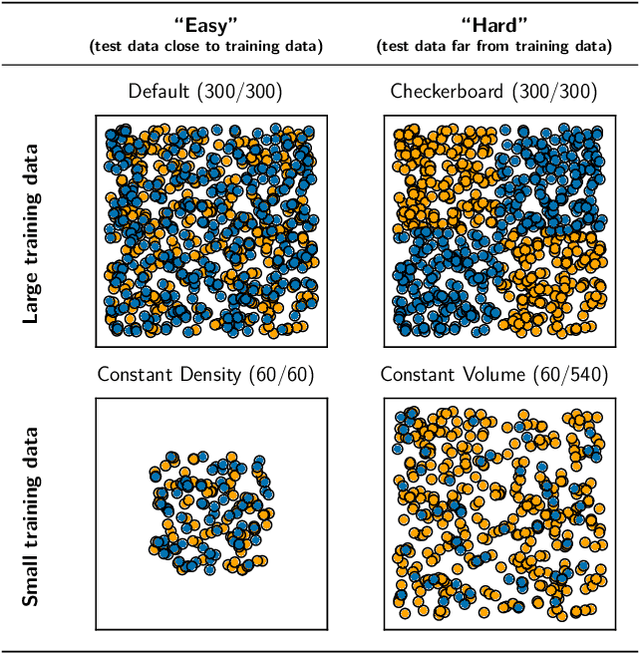
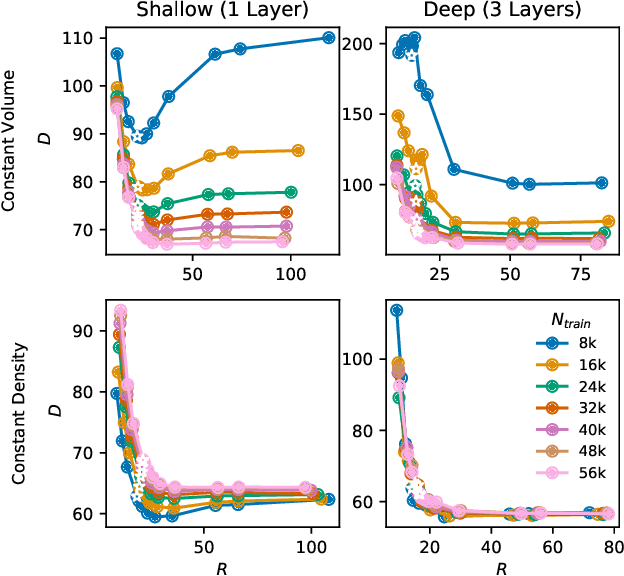
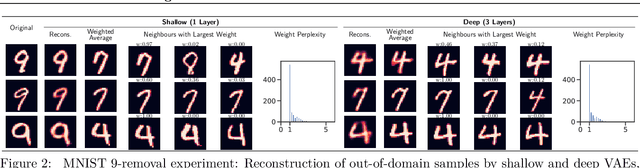

Abstract:We evaluate the ability of variational autoencoders to generalize to unseen examples in domains with a large combinatorial space of feature values. Our experiments systematically evaluate the effect of network width, depth, regularization, and the typical distance between the training and test examples. Increasing network capacity benefits generalization in easy problems, where test-set examples are similar to training examples. In more difficult problems, increasing capacity deteriorates generalization when optimizing the standard VAE objective, but once again improves generalization when we decrease the KL regularization. Our results establish that interplay between model capacity and KL regularization is not clear cut; we need to take the typical distance between train and test examples into account when evaluating generalization.
Structured Neural Topic Models for Reviews
Jan 02, 2019
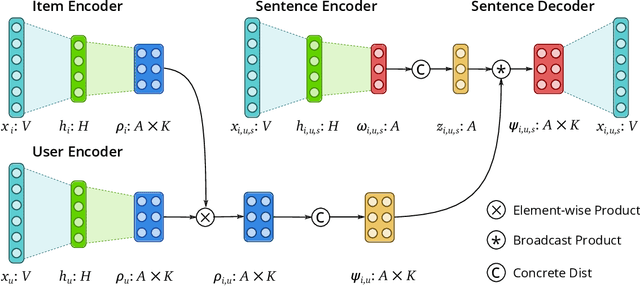

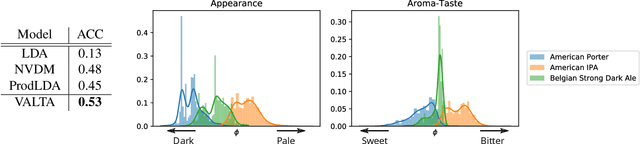
Abstract:We present Variational Aspect-based Latent Topic Allocation (VALTA), a family of autoencoding topic models that learn aspect-based representations of reviews. VALTA defines a user-item encoder that maps bag-of-words vectors for combined reviews associated with each paired user and item onto structured embeddings, which in turn define per-aspect topic weights. We model individual reviews in a structured manner by inferring an aspect assignment for each sentence in a given review, where the per-aspect topic weights obtained by the user-item encoder serve to define a mixture over topics, conditioned on the aspect. The result is an autoencoding neural topic model for reviews, which can be trained in a fully unsupervised manner to learn topics that are structured into aspects. Experimental evaluation on large number of datasets demonstrates that aspects are interpretable, yield higher coherence scores than non-structured autoencoding topic model variants, and can be utilized to perform aspect-based comparison and genre discovery.
Can VAEs Generate Novel Examples?
Dec 22, 2018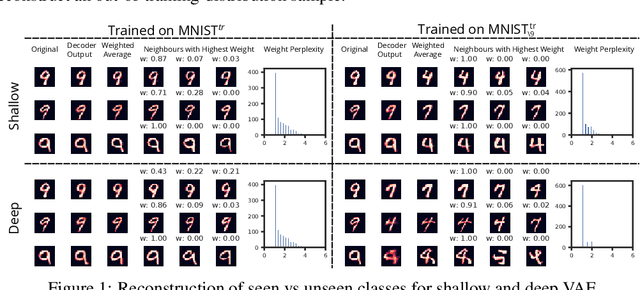
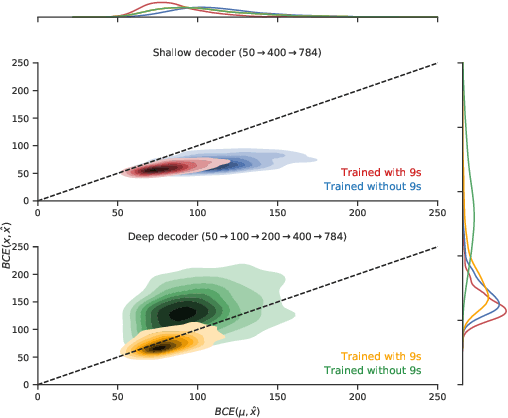

Abstract:An implicit goal in works on deep generative models is that such models should be able to generate novel examples that were not previously seen in the training data. In this paper, we investigate to what extent this property holds for widely employed variational autoencoder (VAE) architectures. VAEs maximize a lower bound on the log marginal likelihood, which implies that they will in principle overfit the training data when provided with a sufficiently expressive decoder. In the limit of an infinite capacity decoder, the optimal generative model is a uniform mixture over the training data. More generally, an optimal decoder should output a weighted average over the examples in the training data, where the magnitude of the weights is determined by the proximity in the latent space. This leads to the hypothesis that, for a sufficiently high capacity encoder and decoder, the VAE decoder will perform nearest-neighbor matching according to the coordinates in the latent space. To test this hypothesis, we investigate generalization on the MNIST dataset. We consider both generalization to new examples of previously seen classes, and generalization to the classes that were withheld from the training set. In both cases, we find that reconstructions are closely approximated by nearest neighbors for higher-dimensional parameterizations. When generalizing to unseen classes however, lower-dimensional parameterizations offer a clear advantage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge