On computable learning of continuous features

We introduce definitions of computable PAC learning for binary classification over computable metric spaces. We provide sufficient conditions for learners that are empirical risk minimizers (ERM) to be computable, and bound the strong Weihrauch degree of an ERM learner under more general conditions. We also give a presentation of a hypothesis class that does not admit any proper computable PAC learner with computable sample function, despite the underlying class being PAC learnable.

Conjugate Energy-Based Models

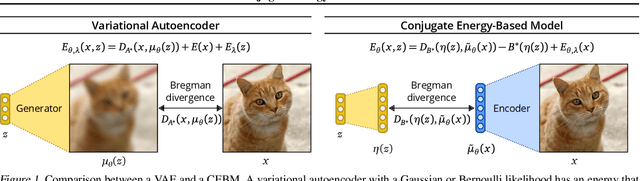
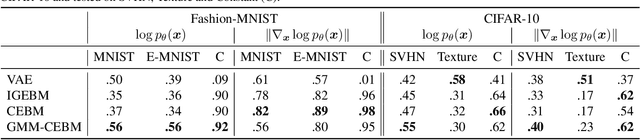
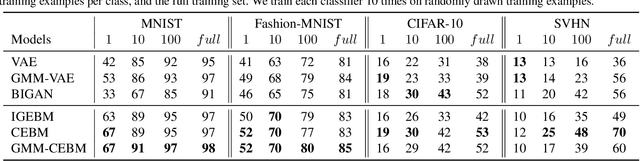
In this paper, we propose conjugate energy-based models (CEBMs), a new class of energy-based models that define a joint density over data and latent variables. The joint density of a CEBM decomposes into an intractable distribution over data and a tractable posterior over latent variables. CEBMs have similar use cases as variational autoencoders, in the sense that they learn an unsupervised mapping from data to latent variables. However, these models omit a generator network, which allows them to learn more flexible notions of similarity between data points. Our experiments demonstrate that conjugate EBMs achieve competitive results in terms of image modelling, predictive power of latent space, and out-of-domain detection on a variety of datasets.

Detecting and Exorcising Statistical Demons from Language Models with Anti-Models of Negative Data

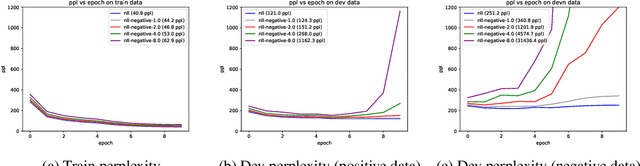
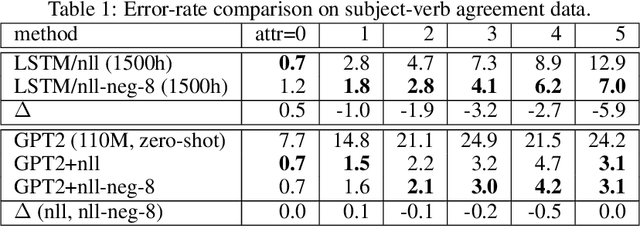
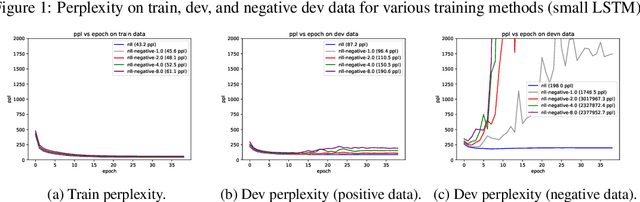
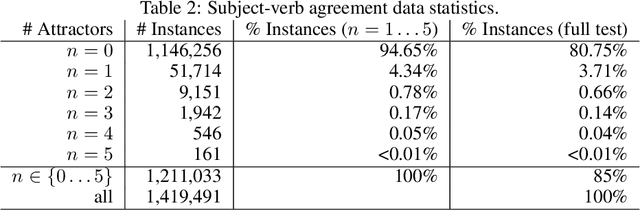
It's been said that "Language Models are Unsupervised Multitask Learners." Indeed, self-supervised language models trained on "positive" examples of English text generalize in desirable ways to many natural language tasks. But if such models can stray so far from an initial self-supervision objective, a wayward model might generalize in undesirable ways too, say to nonsensical "negative" examples of unnatural language. A key question in this work is: do language models trained on (positive) training data also generalize to (negative) test data? We use this question as a contrivance to assess the extent to which language models learn undesirable properties of text, such as n-grams, that might interfere with the learning of more desirable properties of text, such as syntax. We find that within a model family, as the number of parameters, training epochs, and data set size increase, so does a model's ability to generalize to negative n-gram data, indicating standard self-supervision generalizes too far. We propose a form of inductive bias that attenuates such undesirable signals with negative data distributions automatically learned from positive data. We apply the method to remove n-gram signals from LSTMs and find that doing so causes them to favor syntactic signals, as demonstrated by large error reductions (up to 46% on the hardest cases) on a syntactic subject-verb agreement task.

Verification of ML Systems via Reparameterization

As machine learning is increasingly used in essential systems, it is important to reduce or eliminate the incidence of serious bugs. A growing body of research has developed machine learning algorithms with formal guarantees about performance, robustness, or fairness. Yet, the analysis of these algorithms is often complex, and implementing such systems in practice introduces room for error. Proof assistants can be used to formally verify machine learning systems by constructing machine checked proofs of correctness that rule out such bugs. However, reasoning about probabilistic claims inside of a proof assistant remains challenging. We show how a probabilistic program can be automatically represented in a theorem prover using the concept of \emph{reparameterization}, and how some of the tedious proofs of measurability can be generated automatically from the probabilistic program. To demonstrate that this approach is broad enough to handle rather different types of machine learning systems, we verify both a classic result from statistical learning theory (PAC-learnability of decision stumps) and prove that the null model used in a Bayesian hypothesis test satisfies a fairness criterion called demographic parity.

A Formal Proof of PAC Learnability for Decision Stumps

We present a machine-checked, formal proof of PAC learnability of the concept class of decision stumps. A formal proof has every step checked and justified using fundamental axioms of mathematics. We construct and check our proof using the Lean theorem prover. Though such a proof appears simple, a few analytic and measure-theoretic subtleties arise when carrying it out fully formally. We explain how we can cleanly separate out the parts that deal with these subtleties by using Lean features and a category theoretic construction called the Giry monad.

Sketching for Latent Dirichlet-Categorical Models

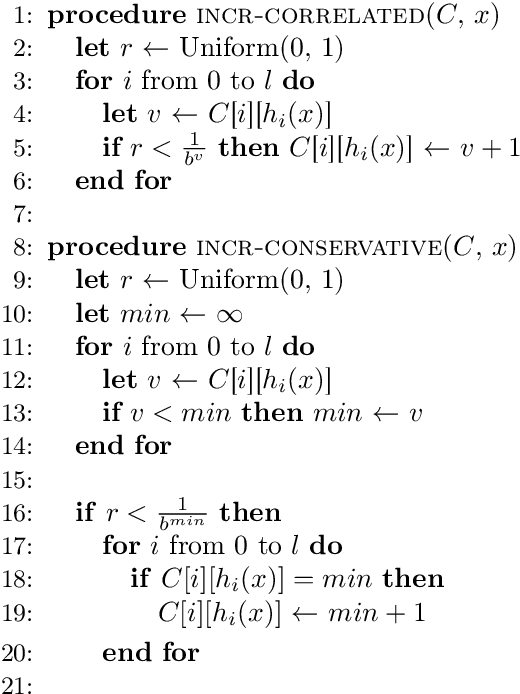
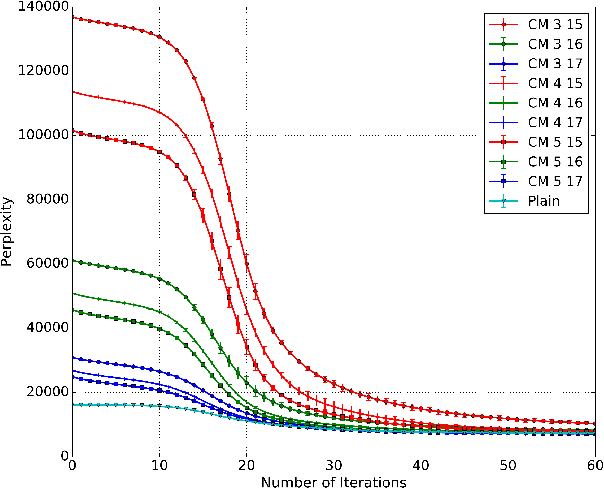
Recent work has explored transforming data sets into smaller, approximate summaries in order to scale Bayesian inference. We examine a related problem in which the parameters of a Bayesian model are very large and expensive to store in memory, and propose more compact representations of parameter values that can be used during inference. We focus on a class of graphical models that we refer to as latent Dirichlet-Categorical models, and show how a combination of two sketching algorithms known as count-min sketch and approximate counters provide an efficient representation for them. We show that this sketch combination -- which, despite having been used before in NLP applications, has not been previously analyzed -- enjoys desirable properties. We prove that for this class of models, when the sketches are used during Markov Chain Monte Carlo inference, the equilibrium of sketched MCMC converges to that of the exact chain as sketch parameters are tuned to reduce the error rate.

Gradient-based Inference for Networks with Output Constraints

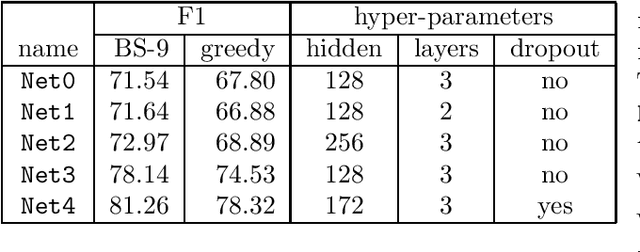
Practitioners apply neural networks to increasingly complex problems in natural language processing (NLP), such as syntactic parsing that have rich output structures. Many such structured-prediction problems require deterministic constraints on the output values; for example, in sequence-to-sequence syntactic parsing, we require that the sequential outputs encode valid trees. While hidden units might capture such properties, the network is not always able to learn such constraints from the training data alone, and practitioners must then resort to post-processing. In this paper, we present an inference method for neural networks that enforces deterministic constraints on outputs without performing rule-based post-processing or expensive discrete search. Instead, in the spirit of gradient-based training, we enforce constraints with gradient-based inference: for each input at test-time, we nudge continuous weights until the network's unconstrained inference procedure generates an output that satisfies the constraints. We apply our methods to three tasks with hard constraints: sequence transduction, constituency parsing, and semantic role labeling (SRL). In each case, the algorithm not only satisfies constraints but improves accuracy, even when the underlying network is state-of-the-art.

Augur: a Modeling Language for Data-Parallel Probabilistic Inference

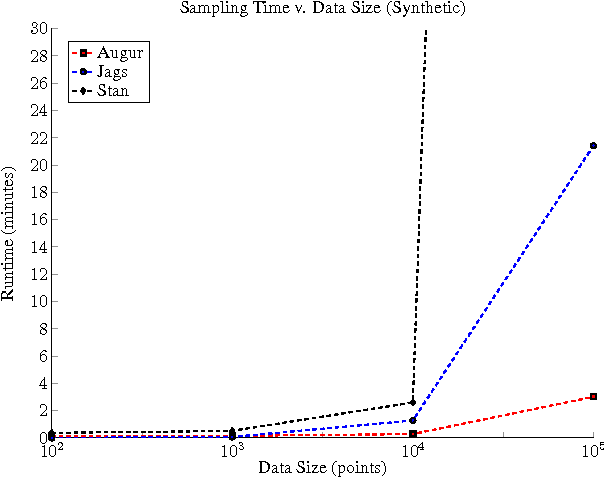
It is time-consuming and error-prone to implement inference procedures for each new probabilistic model. Probabilistic programming addresses this problem by allowing a user to specify the model and having a compiler automatically generate an inference procedure for it. For this approach to be practical, it is important to generate inference code that has reasonable performance. In this paper, we present a probabilistic programming language and compiler for Bayesian networks designed to make effective use of data-parallel architectures such as GPUs. Our language is fully integrated within the Scala programming language and benefits from tools such as IDE support, type-checking, and code completion. We show that the compiler can generate data-parallel inference code scalable to thousands of GPU cores by making use of the conditional independence relationships in the Bayesian network.