Detecting and Exorcising Statistical Demons from Language Models with Anti-Models of Negative Data

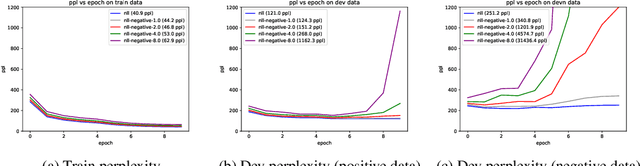
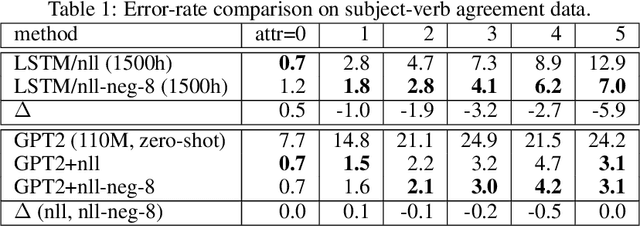
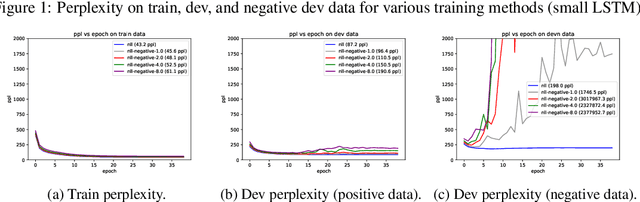
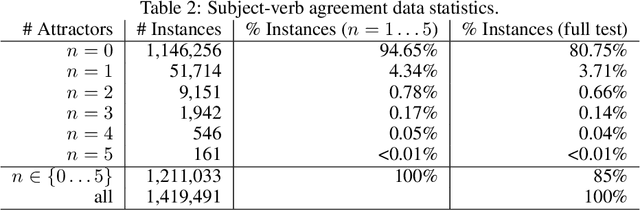
It's been said that "Language Models are Unsupervised Multitask Learners." Indeed, self-supervised language models trained on "positive" examples of English text generalize in desirable ways to many natural language tasks. But if such models can stray so far from an initial self-supervision objective, a wayward model might generalize in undesirable ways too, say to nonsensical "negative" examples of unnatural language. A key question in this work is: do language models trained on (positive) training data also generalize to (negative) test data? We use this question as a contrivance to assess the extent to which language models learn undesirable properties of text, such as n-grams, that might interfere with the learning of more desirable properties of text, such as syntax. We find that within a model family, as the number of parameters, training epochs, and data set size increase, so does a model's ability to generalize to negative n-gram data, indicating standard self-supervision generalizes too far. We propose a form of inductive bias that attenuates such undesirable signals with negative data distributions automatically learned from positive data. We apply the method to remove n-gram signals from LSTMs and find that doing so causes them to favor syntactic signals, as demonstrated by large error reductions (up to 46% on the hardest cases) on a syntactic subject-verb agreement task.

Verification of ML Systems via Reparameterization

As machine learning is increasingly used in essential systems, it is important to reduce or eliminate the incidence of serious bugs. A growing body of research has developed machine learning algorithms with formal guarantees about performance, robustness, or fairness. Yet, the analysis of these algorithms is often complex, and implementing such systems in practice introduces room for error. Proof assistants can be used to formally verify machine learning systems by constructing machine checked proofs of correctness that rule out such bugs. However, reasoning about probabilistic claims inside of a proof assistant remains challenging. We show how a probabilistic program can be automatically represented in a theorem prover using the concept of \emph{reparameterization}, and how some of the tedious proofs of measurability can be generated automatically from the probabilistic program. To demonstrate that this approach is broad enough to handle rather different types of machine learning systems, we verify both a classic result from statistical learning theory (PAC-learnability of decision stumps) and prove that the null model used in a Bayesian hypothesis test satisfies a fairness criterion called demographic parity.

Filling in the details: Perceiving from low fidelity images

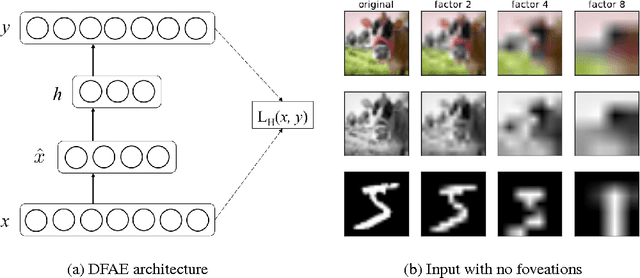
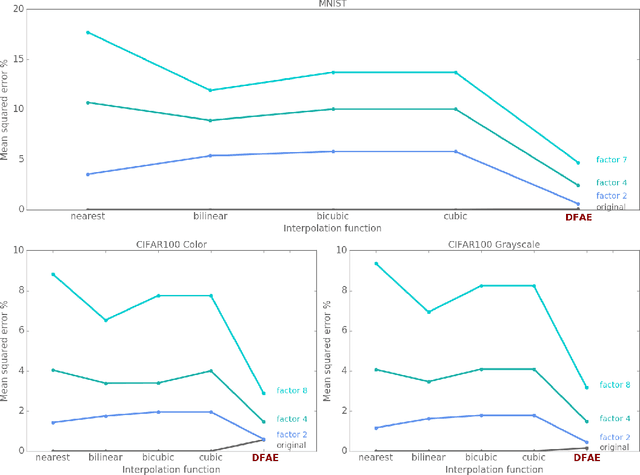
Humans perceive their surroundings in great detail even though most of our visual field is reduced to low-fidelity color-deprived (e.g. dichromatic) input by the retina. In contrast, most deep learning architectures are computationally wasteful in that they consider every part of the input when performing an image processing task. Yet, the human visual system is able to perform visual reasoning despite having only a small fovea of high visual acuity. With this in mind, we wish to understand the extent to which connectionist architectures are able to learn from and reason with low acuity, distorted inputs. Specifically, we train autoencoders to generate full-detail images from low-detail "foveations" of those images and then measure their ability to reconstruct the full-detail images from the foveated versions. By varying the type of foveation, we can study how well the architectures can cope with various types of distortion. We find that the autoencoder compensates for lower detail by learning increasingly global feature functions. In many cases, the learnt features are suitable for reconstructing the original full-detail image. For example, we find that the networks accurately perceive color in the periphery, even when 75\% of the input is achromatic.