Verification of ML Systems via Reparameterization

As machine learning is increasingly used in essential systems, it is important to reduce or eliminate the incidence of serious bugs. A growing body of research has developed machine learning algorithms with formal guarantees about performance, robustness, or fairness. Yet, the analysis of these algorithms is often complex, and implementing such systems in practice introduces room for error. Proof assistants can be used to formally verify machine learning systems by constructing machine checked proofs of correctness that rule out such bugs. However, reasoning about probabilistic claims inside of a proof assistant remains challenging. We show how a probabilistic program can be automatically represented in a theorem prover using the concept of \emph{reparameterization}, and how some of the tedious proofs of measurability can be generated automatically from the probabilistic program. To demonstrate that this approach is broad enough to handle rather different types of machine learning systems, we verify both a classic result from statistical learning theory (PAC-learnability of decision stumps) and prove that the null model used in a Bayesian hypothesis test satisfies a fairness criterion called demographic parity.

A Formal Proof of PAC Learnability for Decision Stumps

We present a machine-checked, formal proof of PAC learnability of the concept class of decision stumps. A formal proof has every step checked and justified using fundamental axioms of mathematics. We construct and check our proof using the Lean theorem prover. Though such a proof appears simple, a few analytic and measure-theoretic subtleties arise when carrying it out fully formally. We explain how we can cleanly separate out the parts that deal with these subtleties by using Lean features and a category theoretic construction called the Giry monad.

Sketching for Latent Dirichlet-Categorical Models

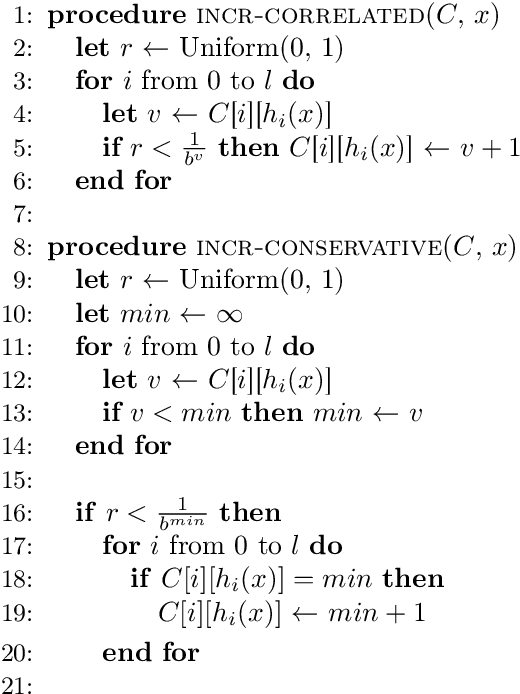
Recent work has explored transforming data sets into smaller, approximate summaries in order to scale Bayesian inference. We examine a related problem in which the parameters of a Bayesian model are very large and expensive to store in memory, and propose more compact representations of parameter values that can be used during inference. We focus on a class of graphical models that we refer to as latent Dirichlet-Categorical models, and show how a combination of two sketching algorithms known as count-min sketch and approximate counters provide an efficient representation for them. We show that this sketch combination -- which, despite having been used before in NLP applications, has not been previously analyzed -- enjoys desirable properties. We prove that for this class of models, when the sketches are used during Markov Chain Monte Carlo inference, the equilibrium of sketched MCMC converges to that of the exact chain as sketch parameters are tuned to reduce the error rate.

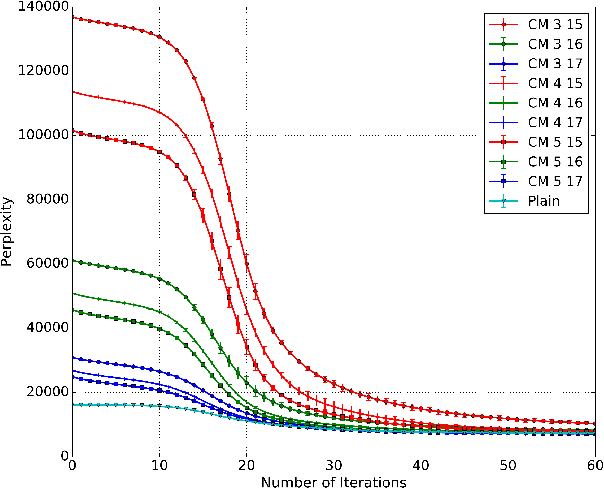
Augur: a Modeling Language for Data-Parallel Probabilistic Inference

It is time-consuming and error-prone to implement inference procedures for each new probabilistic model. Probabilistic programming addresses this problem by allowing a user to specify the model and having a compiler automatically generate an inference procedure for it. For this approach to be practical, it is important to generate inference code that has reasonable performance. In this paper, we present a probabilistic programming language and compiler for Bayesian networks designed to make effective use of data-parallel architectures such as GPUs. Our language is fully integrated within the Scala programming language and benefits from tools such as IDE support, type-checking, and code completion. We show that the compiler can generate data-parallel inference code scalable to thousands of GPU cores by making use of the conditional independence relationships in the Bayesian network.