A Computational Approach to Analyzing Language Change and Variation in the Constructed Language Toki Pona

This study explores language change and variation in Toki Pona, a constructed language with approximately 120 core words. Taking a computational and corpus-based approach, the study examines features including fluid word classes and transitivity in order to examine (1) changes in preferences of content words for different syntactic positions over time and (2) variation in usage across different corpora. The results suggest that sociolinguistic factors influence Toki Pona in the same way as natural languages, and that even constructed linguistic systems naturally evolve as communities use them.

Scaling Gaussian Process Regression with Full Derivative Observations

We present a scalable Gaussian Process (GP) method that can fit and predict full derivative observations called DSoftKI. It extends SoftKI, a method that approximates a kernel via softmax interpolation from learned interpolation point locations, to the setting with derivatives. DSoftKI enhances SoftKI's interpolation scheme to incorporate the directional orientation of interpolation points relative to the data. This enables the construction of a scalable approximate kernel, including its first and second-order derivatives, through interpolation. We evaluate DSoftKI on a synthetic function benchmark and high-dimensional molecular force field prediction (100-1000 dimensions), demonstrating that DSoftKI is accurate and can scale to larger datasets with full derivative observations than previously possible.

High-Dimensional Gaussian Process Regression with Soft Kernel Interpolation

We introduce Soft Kernel Interpolation (SoftKI) designed for scalable Gaussian Process (GP) regression on high-dimensional datasets. Inspired by Structured Kernel Interpolation (SKI), which approximates a GP kernel via interpolation from a structured lattice, SoftKI approximates a kernel via softmax interpolation from a smaller number of learned interpolation (i.e, inducing) points. By abandoning the lattice structure used in SKI-based methods, SoftKI separates the cost of forming an approximate GP kernel from the dimensionality of the data, making it well-suited for high-dimensional datasets. We demonstrate the effectiveness of SoftKI across various examples, and demonstrate that its accuracy exceeds that of other scalable GP methods when the data dimensionality is modest (around $10$).

On Training Derivative-Constrained Neural Networks

We refer to the setting where the (partial) derivatives of a neural network's (NN's) predictions with respect to its inputs are used as additional training signal as a derivative-constrained (DC) NN. This situation is common in physics-informed settings in the natural sciences. We propose an integrated RELU (IReLU) activation function to improve training of DC NNs. We also investigate denormalization and label rescaling to help stabilize DC training. We evaluate our methods on physics-informed settings including quantum chemistry and Scientific Machine Learning (SciML) tasks. We demonstrate that existing architectures with IReLU activations combined with denormalization and label rescaling better incorporate training signal provided by derivative constraints.

ExpeL: LLM Agents Are Experiential Learners

The recent surge in research interest in applying large language models (LLMs) to decision-making tasks has flourished by leveraging the extensive world knowledge embedded in LLMs. While there is a growing demand to tailor LLMs for custom decision-making tasks, finetuning them for specific tasks is resource-intensive and may diminish the model's generalization capabilities. Moreover, state-of-the-art language models like GPT-4 and Claude are primarily accessible through API calls, with their parametric weights remaining proprietary and unavailable to the public. This scenario emphasizes the growing need for new methodologies that allow learning from agent experiences without requiring parametric updates. To address these problems, we introduce the Experiential Learning (ExpeL) agent. Our agent autonomously gathers experiences and extracts knowledge using natural language from a collection of training tasks. At inference, the agent recalls its extracted insights and past experiences to make informed decisions. Our empirical results highlight the robust learning efficacy of the ExpeL agent, indicating a consistent enhancement in its performance as it accumulates experiences. We further explore the emerging capabilities and transfer learning potential of the ExpeL agent through qualitative observations and additional experiments.

Pus$\mathbb{H}$: Concurrent Probabilistic Programming with Function Spaces

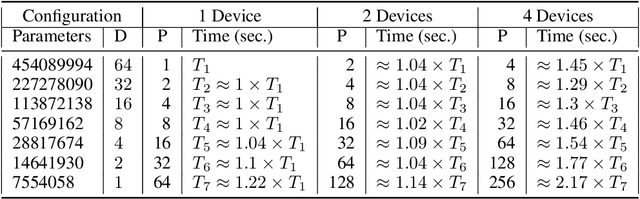
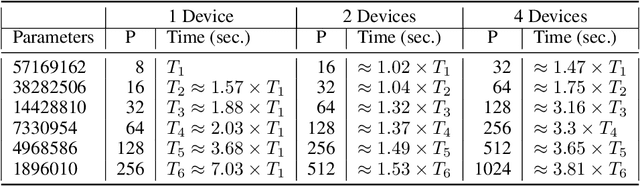
We introduce a prototype probabilistic programming language (PPL) called Pus$\mathbb{H}$ for performing Bayesian inference on function spaces with a focus on Bayesian deep learning (BDL). We describe the core abstraction of Pus$\mathbb{H}$ based on particles that links models, specified as neural networks (NNs), with inference, specified as procedures on particles using a programming model inspired by message passing. Finally, we test Pus$\mathbb{H}$ on a variety of models and datasets used in scientific machine learning (SciML), a domain with natural function space inference problems, and we evaluate scaling of Pus$\mathbb{H}$ on single-node multi-GPU devices. Thus we explore the combination of probabilistic programming, NNs, and concurrency in the context of Bayesian inference on function spaces. The code can be found at https://github.com/lbai-lab/PusH.

On Learning to Prove

In this paper, we consider the problem of learning a (first-order) theorem prover where we use a representation of beliefs in mathematical claims instead of a proof system to search for proofs. The inspiration for doing so comes from the practices of human mathematicians where a proof system is typically used after the fact to justify a sequence of intuitive steps obtained by "plausible reasoning" rather than to discover them. Towards this end, we introduce a probabilistic representation of beliefs in first-order statements based on first-order distributive normal forms (dnfs) devised by the philosopher Jaakko Hintikka. Notably, the representation supports Bayesian update and does not enforce that logically equivalent statements are assigned the same probability---otherwise, we would end up in a circular situation where we require a prover in order to assign beliefs. We then examine (1) conjecturing as (statistical) model selection and (2) an alternating-turn proving game amenable (in principle) to self-play training to learn a prover that is both complete in the limit and sound provided that players maintain "reasonable" beliefs. Dnfs have super-exponential space requirements so the ideas in this paper should be taken as conducting a thought experiment on "learning to prove". As a step towards making the ideas practical, we will comment on how abstractions can be used to control the space requirements at the cost of completeness.

GamePad: A Learning Environment for Theorem Proving

In this paper, we introduce a system called GamePad that can be used to explore the application of machine learning methods to theorem proving in the Coq proof assistant. Interactive theorem provers such as Coq enable users to construct machine-checkable proofs in a step-by-step manner. Hence, they provide an opportunity to explore theorem proving at a human level of abstraction. We use GamePad to synthesize proofs for a simple algebraic rewrite problem and train baseline models for a formalization of the Feit-Thompson theorem. We address position evaluation (i.e., predict the number of proof steps left) and tactic prediction (i.e., predict the next proof step) tasks, which arise naturally in human-level theorem proving.

Augur: a Modeling Language for Data-Parallel Probabilistic Inference

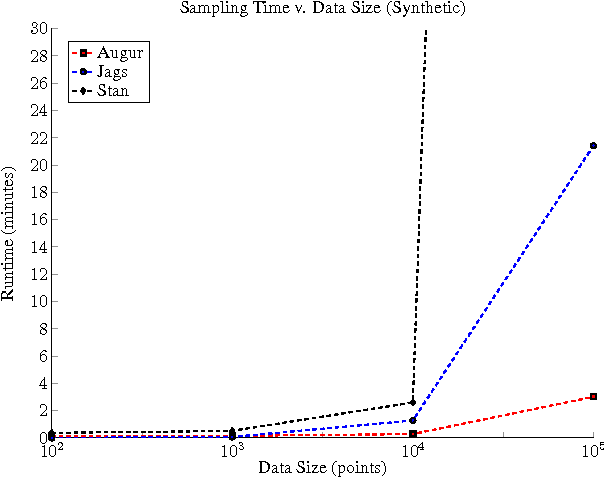
It is time-consuming and error-prone to implement inference procedures for each new probabilistic model. Probabilistic programming addresses this problem by allowing a user to specify the model and having a compiler automatically generate an inference procedure for it. For this approach to be practical, it is important to generate inference code that has reasonable performance. In this paper, we present a probabilistic programming language and compiler for Bayesian networks designed to make effective use of data-parallel architectures such as GPUs. Our language is fully integrated within the Scala programming language and benefits from tools such as IDE support, type-checking, and code completion. We show that the compiler can generate data-parallel inference code scalable to thousands of GPU cores by making use of the conditional independence relationships in the Bayesian network.