Variational Stochastic Gradient Descent for Deep Neural Networks
Paper and Code
Apr 09, 2024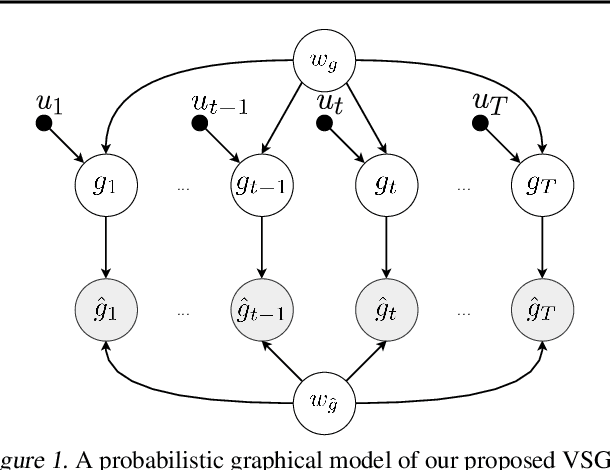
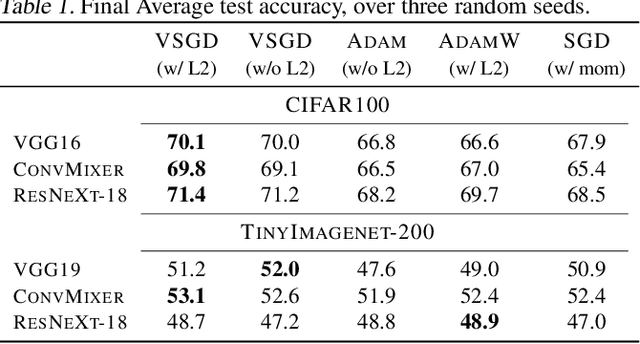
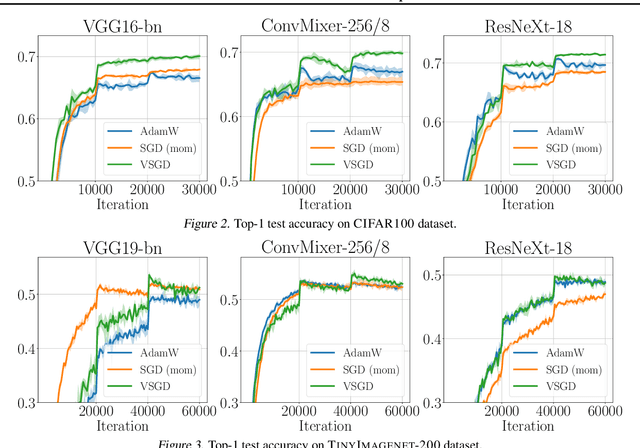
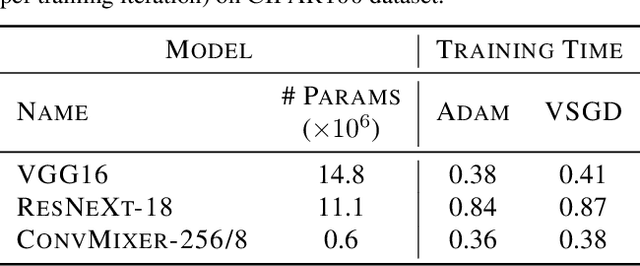
Optimizing deep neural networks is one of the main tasks in successful deep learning. Current state-of-the-art optimizers are adaptive gradient-based optimization methods such as Adam. Recently, there has been an increasing interest in formulating gradient-based optimizers in a probabilistic framework for better estimation of gradients and modeling uncertainties. Here, we propose to combine both approaches, resulting in the Variational Stochastic Gradient Descent (VSGD) optimizer. We model gradient updates as a probabilistic model and utilize stochastic variational inference (SVI) to derive an efficient and effective update rule. Further, we show how our VSGD method relates to other adaptive gradient-based optimizers like Adam. Lastly, we carry out experiments on two image classification datasets and four deep neural network architectures, where we show that VSGD outperforms Adam and SGD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge