SigFormer: Signature Transformers for Deep Hedging

Deep hedging is a promising direction in quantitative finance, incorporating models and techniques from deep learning research. While giving excellent hedging strategies, models inherently requires careful treatment in designing architectures for neural networks. To mitigate such difficulties, we introduce SigFormer, a novel deep learning model that combines the power of path signatures and transformers to handle sequential data, particularly in cases with irregularities. Path signatures effectively capture complex data patterns, while transformers provide superior sequential attention. Our proposed model is empirically compared to existing methods on synthetic data, showcasing faster learning and enhanced robustness, especially in the presence of irregular underlying price data. Additionally, we validate our model performance through a real-world backtest on hedging the SP 500 index, demonstrating positive outcomes.

Conditional Support Alignment for Domain Adaptation with Label Shift

Unsupervised domain adaptation (UDA) refers to a domain adaptation framework in which a learning model is trained based on the labeled samples on the source domain and unlabelled ones in the target domain. The dominant existing methods in the field that rely on the classical covariate shift assumption to learn domain-invariant feature representation have yielded suboptimal performance under the label distribution shift between source and target domains. In this paper, we propose a novel conditional adversarial support alignment (CASA) whose aim is to minimize the conditional symmetric support divergence between the source's and target domain's feature representation distributions, aiming at a more helpful representation for the classification task. We also introduce a novel theoretical target risk bound, which justifies the merits of aligning the supports of conditional feature distributions compared to the existing marginal support alignment approach in the UDA settings. We then provide a complete training process for learning in which the objective optimization functions are precisely based on the proposed target risk bound. Our empirical results demonstrate that CASA outperforms other state-of-the-art methods on different UDA benchmark tasks under label shift conditions.

Learning Compositional Sparse Gaussian Processes with a Shrinkage Prior

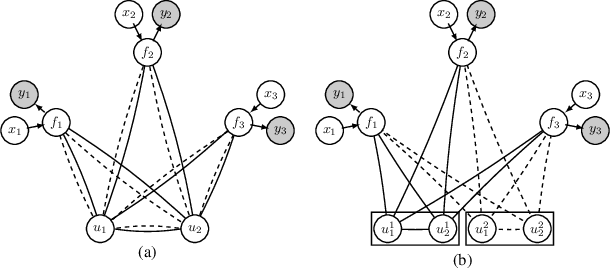
Choosing a proper set of kernel functions is an important problem in learning Gaussian Process (GP) models since each kernel structure has different model complexity and data fitness. Recently, automatic kernel composition methods provide not only accurate prediction but also attractive interpretability through search-based methods. However, existing methods suffer from slow kernel composition learning. To tackle large-scaled data, we propose a new sparse approximate posterior for GPs, MultiSVGP, constructed from groups of inducing points associated with individual additive kernels in compositional kernels. We demonstrate that this approximation provides a better fit to learn compositional kernels given empirical observations. We also theoretically justification on error bound when compared to the traditional sparse GP. In contrast to the search-based approach, we present a novel probabilistic algorithm to learn a kernel composition by handling the sparsity in the kernel selection with Horseshoe prior. We demonstrate that our model can capture characteristics of time series with significant reductions in computational time and have competitive regression performance on real-world data sets.

Characterizing Deep Gaussian Processes via Nonlinear Recurrence Systems

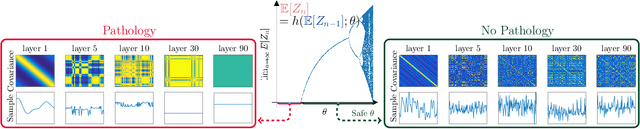
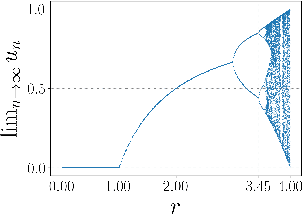
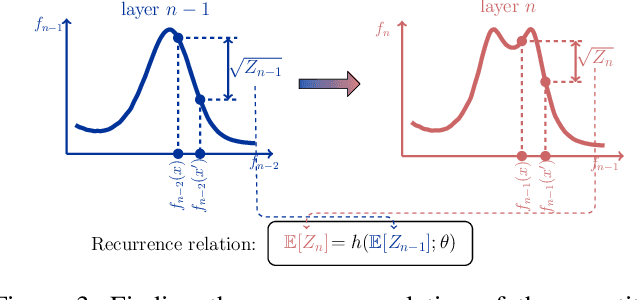
Recent advances in Deep Gaussian Processes (DGPs) show the potential to have more expressive representation than that of traditional Gaussian Processes (GPs). However, there exists a pathology of deep Gaussian processes that their learning capacities reduce significantly when the number of layers increases. In this paper, we present a new analysis in DGPs by studying its corresponding nonlinear dynamic systems to explain the issue. Existing work reports the pathology for the squared exponential kernel function. We extend our investigation to four types of common stationary kernel functions. The recurrence relations between layers are analytically derived, providing a tighter bound and the rate of convergence of the dynamic systems. We demonstrate our finding with a number of experimental results.

Confirmatory Bayesian Online Change Point Detection in the Covariance Structure of Gaussian Processes

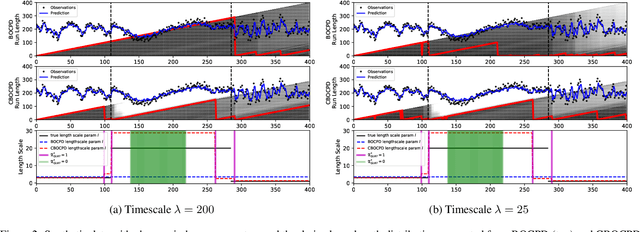
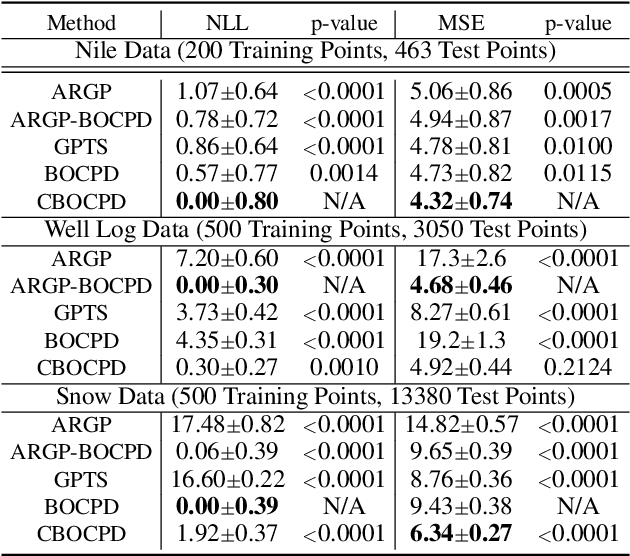
In the analysis of sequential data, the detection of abrupt changes is important in predicting future changes. In this paper, we propose statistical hypothesis tests for detecting covariance structure changes in locally smooth time series modeled by Gaussian Processes (GPs). We provide theoretically justified thresholds for the tests, and use them to improve Bayesian Online Change Point Detection (BOCPD) by confirming statistically significant changes and non-changes. Our Confirmatory BOCPD (CBOCPD) algorithm finds multiple structural breaks in GPs even when hyperparameters are not tuned precisely. We also provide conditions under which CBOCPD provides the lower prediction error compared to BOCPD. Experimental results on synthetic and real-world datasets show that our new tests correctly detect changes in the covariance structure in GPs. The proposed algorithm also outperforms existing methods for the prediction of nonstationarity in terms of both regression error and log likelihood.

Discovering Relational Covariance Structures for Explaining Multiple Time Series

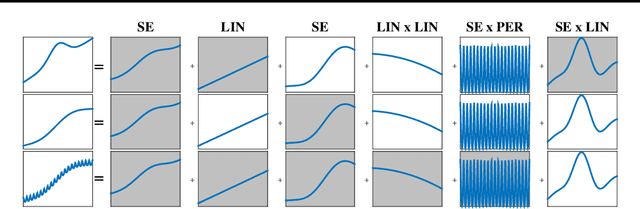
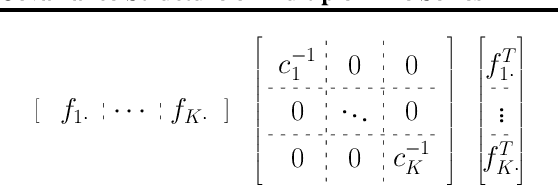
Analyzing time series data is important to predict future events and changes in finance, manufacturing, and administrative decisions. In time series analysis, Gaussian Process (GP) regression methods recently demonstrate competitive performance by decomposing temporal covariance structures. The covariance structure decomposition allows exploiting shared parameters over a set of multiple, selected time series. In this paper, we present two novel GP models which naturally handle multiple time series by placing an Indian Buffet Process (IBP) prior on the presence of shared kernels. We also investigate the well-definedness of the models when infinite latent components are introduced. We present a pragmatic search algorithm which explores a larger structure space efficiently than the existing search algorithm. Experiments are conducted on both synthetic data sets and real-world data sets, showing improved results in term of structure discoveries and predictive performances. We further provide a promising application generating comparison reports from our model results.

Automatic Generation of Probabilistic Programming from Time Series Data

Probabilistic programming languages represent complex data with intermingled models in a few lines of code. Efficient inference algorithms in probabilistic programming languages make possible to build unified frameworks to compute interesting probabilities of various large, real-world problems. When the structure of model is given, constructing a probabilistic program is rather straightforward. Thus, main focus have been to learn the best model parameters and compute marginal probabilities. In this paper, we provide a new perspective to build expressive probabilistic program from continue time series data when the structure of model is not given. The intuition behind of our method is to find a descriptive covariance structure of time series data in nonparametric Gaussian process regression. We report that such descriptive covariance structure efficiently derives a probabilistic programming description accurately.

Searching for Topological Symmetry in Data Haystack

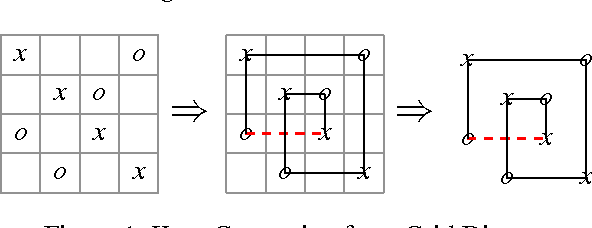
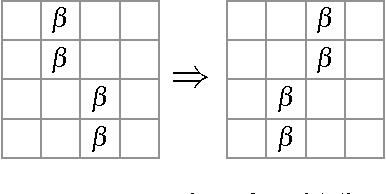
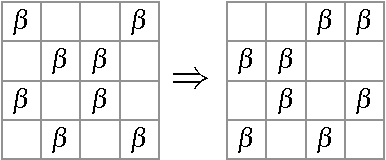
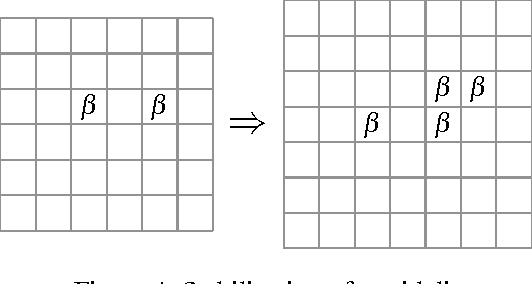
Finding interesting symmetrical topological structures in high-dimensional systems is an important problem in statistical machine learning. Limited amount of available high-dimensional data and its sensitivity to noise pose computational challenges to find symmetry. Our paper presents a new method to find local symmetries in a low-dimensional 2-D grid structure which is embedded in high-dimensional structure. To compute the symmetry in a grid structure, we introduce three legal grid moves (i) Commutation (ii) Cyclic Permutation (iii) Stabilization on sets of local grid squares, grid blocks. The three grid moves are legal transformations as they preserve the statistical distribution of hamming distances in each grid block. We propose and coin the term of grid symmetry of data on the 2-D data grid as the invariance of statistical distributions of hamming distance are preserved after a sequence of grid moves. We have computed and analyzed the grid symmetry of data on multivariate Gaussian distributions and Gamma distributions with noise.

The Automatic Statistician: A Relational Perspective

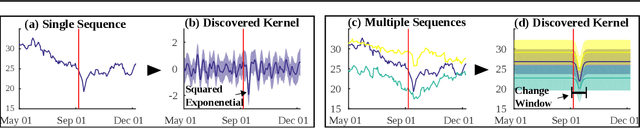
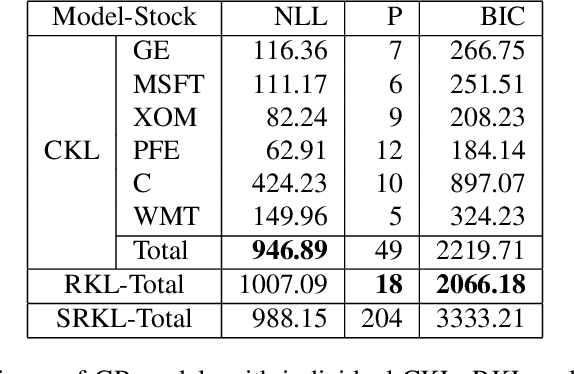
Gaussian Processes (GPs) provide a general and analytically tractable way of modeling complex time-varying, nonparametric functions. The Automatic Bayesian Covariance Discovery (ABCD) system constructs natural-language description of time-series data by treating unknown time-series data nonparametrically using GP with a composite covariance kernel function. Unfortunately, learning a composite covariance kernel with a single time-series data set often results in less informative kernel that may not give qualitative, distinctive descriptions of data. We address this challenge by proposing two relational kernel learning methods which can model multiple time-series data sets by finding common, shared causes of changes. We show that the relational kernel learning methods find more accurate models for regression problems on several real-world data sets; US stock data, US house price index data and currency exchange rate data.