The Fairness Stitch: Unveiling the Potential of Model Stitching in Neural Network De-Biasing

The pursuit of fairness in machine learning models has emerged as a critical research challenge in different applications ranging from bank loan approval to face detection. Despite the widespread adoption of artificial intelligence algorithms across various domains, concerns persist regarding the presence of biases and discrimination within these models. To address this pressing issue, this study introduces a novel method called "The Fairness Stitch (TFS)" to enhance fairness in deep learning models. This method combines model stitching and training jointly, while incorporating fairness constraints. In this research, we assess the effectiveness of our proposed method by conducting a comprehensive evaluation of two well-known datasets, CelebA and UTKFace. We systematically compare the performance of our approach with the existing baseline method. Our findings reveal a notable improvement in achieving a balanced trade-off between fairness and performance, highlighting the promising potential of our method to address bias-related challenges and foster equitable outcomes in machine learning models. This paper poses a challenge to the conventional wisdom of the effectiveness of the last layer in deep learning models for de-biasing.

Stress and Adaptation: Applying Anna Karenina Principle in Deep Learning for Image Classification

Image classification with deep neural networks has reached state-of-art with high accuracy. This success is attributed to good internal representation features that bypasses the difficulties of the non-convex optimization problems. We have little understanding of these internal representations, let alone quantifying them. Recent research efforts have focused on alternative theories and explanations of the generalizability of these deep networks. We propose the alternative perturbation of deep models during their training induces changes that lead to transitions to different families. The result is an Anna Karenina Principle AKP for deep learning, in which less generalizable models unhappy families vary more in their representation than more generalizable models happy families paralleling Leo Tolstoy dictum that all happy families look alike, each unhappy family is unhappy in its own way. Anna Karenina principle has been found in systems in a wide range: from the surface of endangered corals exposed to harsh weather to the lungs of patients suffering from fatal diseases of AIDs. In our paper, we have generated artificial perturbations to our model by hot-swapping the activation and loss functions during the training. In this paper, we build a model to classify cancer cells from non-cancer ones. We give theoretical proof that the internal representations of generalizable happy models are similar in the asymptotic limit. Our experiments verify similar representations of generalizable models.

Fair Classification via Transformer Neural Networks: Case Study of an Educational Domain

Educational technologies nowadays increasingly use data and Machine Learning (ML) models. This gives the students, instructors, and administrators support and insights for the optimum policy. However, it is well acknowledged that ML models are subject to bias, which raises concern about the fairness, bias, and discrimination of using these automated ML algorithms in education and its unintended and unforeseen negative consequences. The contribution of bias during the decision-making comes from datasets used for training ML models and the model architecture. This paper presents a preliminary investigation of fairness constraint in transformer neural networks on Law School and Student-Mathematics datasets. The used transformer models transform these raw datasets into a richer representation space of natural language processing (NLP) while solving fairness classification. We have employed fairness metrics for evaluation and check the trade-off between fairness and accuracy. We have reported the various metrics of F1, SPD, EOD, and accuracy for different architectures from the transformer model class.

Pre-Trained Language Transformers are Universal Image Classifiers

Facial images disclose many hidden personal traits such as age, gender, race, health, emotion, and psychology. Understanding these traits will help to classify the people in different attributes. In this paper, we have presented a novel method for classifying images using a pretrained transformer model. We apply the pretrained transformer for the binary classification of facial images in criminal and non-criminal classes. The pretrained transformer of GPT-2 is trained to generate text and then fine-tuned to classify facial images. During the finetuning process with images, most of the layers of GT-2 are frozen during backpropagation and the model is frozen pretrained transformer (FPT). The FPT acts as a universal image classifier, and this paper shows the application of FPT on facial images. We also use our FPT on encrypted images for classification. Our FPT shows high accuracy on both raw facial images and encrypted images. We hypothesize the meta-learning capacity FPT gained because of its large size and trained on a large size with theory and experiments. The GPT-2 trained to generate a single word token at a time, through the autoregressive process, forced to heavy-tail distribution. Then the FPT uses the heavy-tail property as its meta-learning capacity for classifying images. Our work shows one way to avoid bias during the machine classification of images.The FPT encodes worldly knowledge because of the pretraining of one text, which it uses during the classification. The statistical error of classification is reduced because of the added context gained from the text.Our paper shows the ethical dimension of using encrypted data for classification.Criminal images are sensitive to share across the boundary but encrypted largely evades ethical concern.FPT showing good classification accuracy on encrypted images shows promise for further research on privacy-preserving machine learning.

Pretrained Language Models are Symbolic Mathematics Solvers too!

Solving symbolic mathematics has always been of in the arena of human ingenuity that needs compositional reasoning and recurrence. However, recent studies have shown that large-scale language models such as transformers are universal and surprisingly can be trained as a sequence-to-sequence task to solve complex mathematical equations. These large transformer models need humongous amounts of training data to generalize to unseen symbolic mathematics problems. In this paper, we present a sample efficient way of solving the symbolic tasks by first pretraining the transformer model with language translation and then fine-tuning the pretrained transformer model to solve the downstream task of symbolic mathematics. We achieve comparable accuracy on the integration task with our pretrained model while using around $1.5$ orders of magnitude less number of training samples with respect to the state-of-the-art deep learning for symbolic mathematics. The test accuracy on differential equation tasks is considerably lower comparing with integration as they need higher order recursions that are not present in language translations. We pretrain our model with different pairs of language translations. Our results show language bias in solving symbolic mathematics tasks. Finally, we study the robustness of the fine-tuned model on symbolic math tasks against distribution shift, and our approach generalizes better in distribution shift scenarios for the function integration.

Searching for Topological Symmetry in Data Haystack

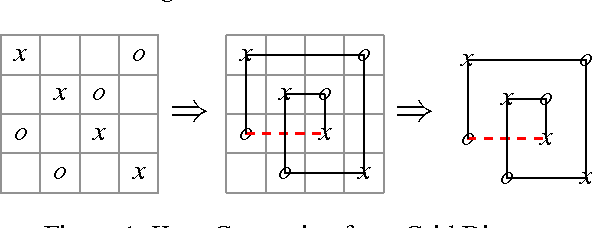
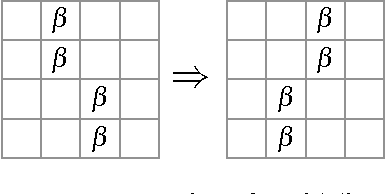
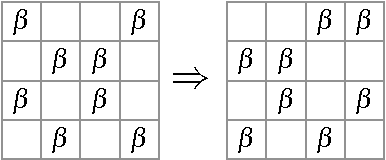
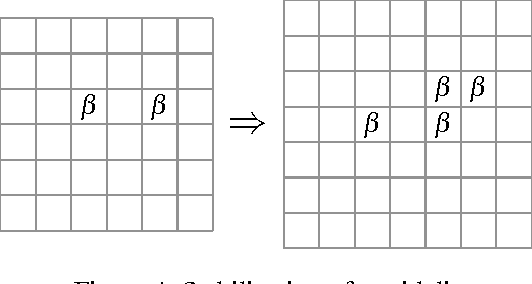
Finding interesting symmetrical topological structures in high-dimensional systems is an important problem in statistical machine learning. Limited amount of available high-dimensional data and its sensitivity to noise pose computational challenges to find symmetry. Our paper presents a new method to find local symmetries in a low-dimensional 2-D grid structure which is embedded in high-dimensional structure. To compute the symmetry in a grid structure, we introduce three legal grid moves (i) Commutation (ii) Cyclic Permutation (iii) Stabilization on sets of local grid squares, grid blocks. The three grid moves are legal transformations as they preserve the statistical distribution of hamming distances in each grid block. We propose and coin the term of grid symmetry of data on the 2-D data grid as the invariance of statistical distributions of hamming distance are preserved after a sequence of grid moves. We have computed and analyzed the grid symmetry of data on multivariate Gaussian distributions and Gamma distributions with noise.