Discovering Relational Covariance Structures for Explaining Multiple Time Series

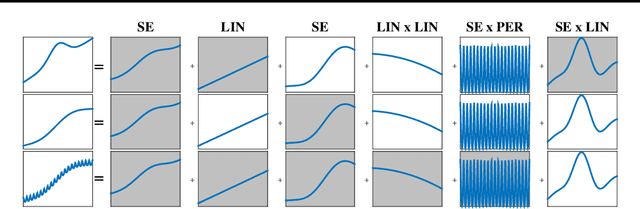
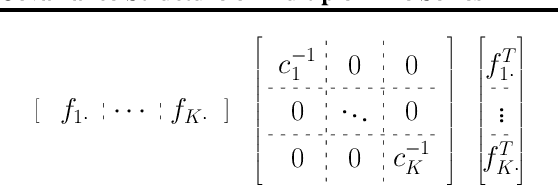
Analyzing time series data is important to predict future events and changes in finance, manufacturing, and administrative decisions. In time series analysis, Gaussian Process (GP) regression methods recently demonstrate competitive performance by decomposing temporal covariance structures. The covariance structure decomposition allows exploiting shared parameters over a set of multiple, selected time series. In this paper, we present two novel GP models which naturally handle multiple time series by placing an Indian Buffet Process (IBP) prior on the presence of shared kernels. We also investigate the well-definedness of the models when infinite latent components are introduced. We present a pragmatic search algorithm which explores a larger structure space efficiently than the existing search algorithm. Experiments are conducted on both synthetic data sets and real-world data sets, showing improved results in term of structure discoveries and predictive performances. We further provide a promising application generating comparison reports from our model results.