Characterizing Deep Gaussian Processes via Nonlinear Recurrence Systems
Paper and Code
Oct 20, 2020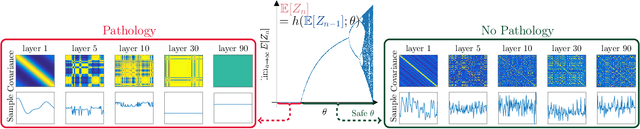
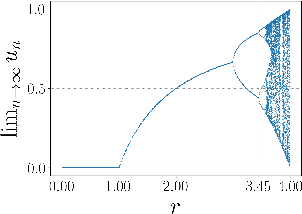

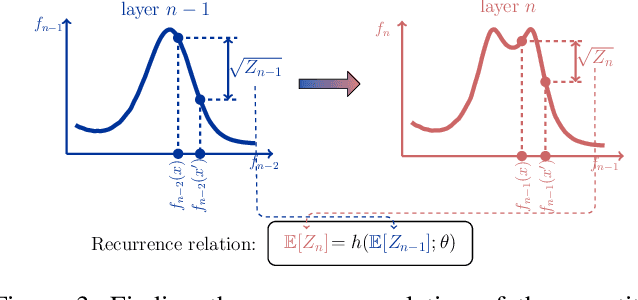
Recent advances in Deep Gaussian Processes (DGPs) show the potential to have more expressive representation than that of traditional Gaussian Processes (GPs). However, there exists a pathology of deep Gaussian processes that their learning capacities reduce significantly when the number of layers increases. In this paper, we present a new analysis in DGPs by studying its corresponding nonlinear dynamic systems to explain the issue. Existing work reports the pathology for the squared exponential kernel function. We extend our investigation to four types of common stationary kernel functions. The recurrence relations between layers are analytically derived, providing a tighter bound and the rate of convergence of the dynamic systems. We demonstrate our finding with a number of experimental results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge