Confirmatory Bayesian Online Change Point Detection in the Covariance Structure of Gaussian Processes
Paper and Code
May 30, 2019

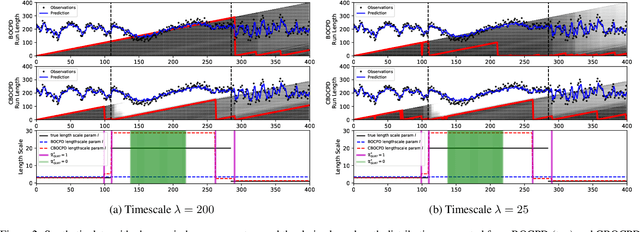
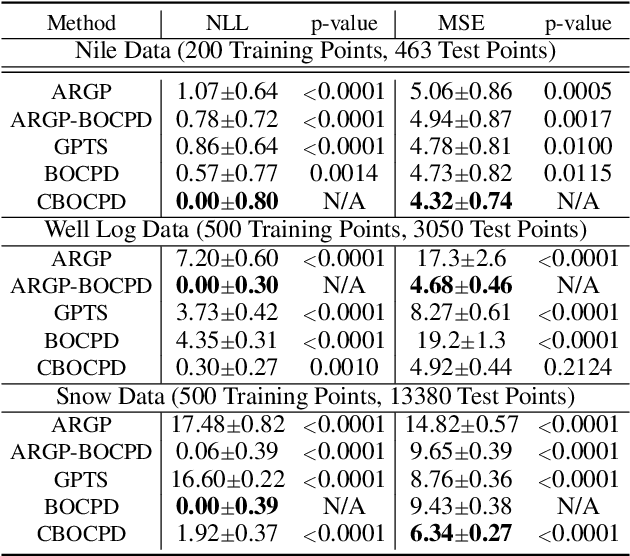
In the analysis of sequential data, the detection of abrupt changes is important in predicting future changes. In this paper, we propose statistical hypothesis tests for detecting covariance structure changes in locally smooth time series modeled by Gaussian Processes (GPs). We provide theoretically justified thresholds for the tests, and use them to improve Bayesian Online Change Point Detection (BOCPD) by confirming statistically significant changes and non-changes. Our Confirmatory BOCPD (CBOCPD) algorithm finds multiple structural breaks in GPs even when hyperparameters are not tuned precisely. We also provide conditions under which CBOCPD provides the lower prediction error compared to BOCPD. Experimental results on synthetic and real-world datasets show that our new tests correctly detect changes in the covariance structure in GPs. The proposed algorithm also outperforms existing methods for the prediction of nonstationarity in terms of both regression error and log likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge