The Automatic Statistician: A Relational Perspective
Paper and Code
Feb 12, 2016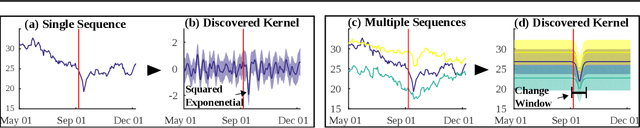
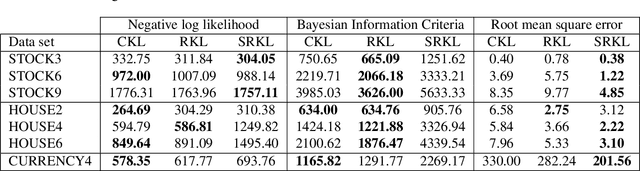
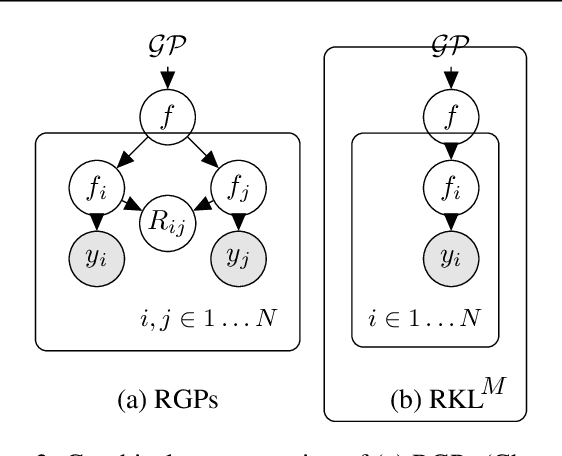
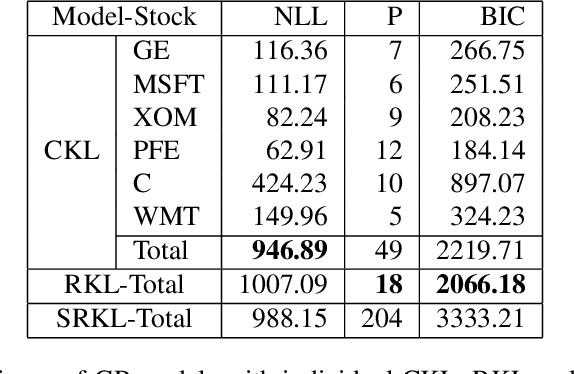
Gaussian Processes (GPs) provide a general and analytically tractable way of modeling complex time-varying, nonparametric functions. The Automatic Bayesian Covariance Discovery (ABCD) system constructs natural-language description of time-series data by treating unknown time-series data nonparametrically using GP with a composite covariance kernel function. Unfortunately, learning a composite covariance kernel with a single time-series data set often results in less informative kernel that may not give qualitative, distinctive descriptions of data. We address this challenge by proposing two relational kernel learning methods which can model multiple time-series data sets by finding common, shared causes of changes. We show that the relational kernel learning methods find more accurate models for regression problems on several real-world data sets; US stock data, US house price index data and currency exchange rate data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge