Cycle Invariant Positional Encoding for Graph Representation Learning

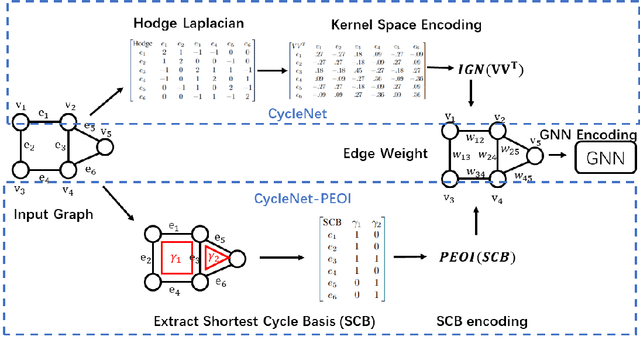
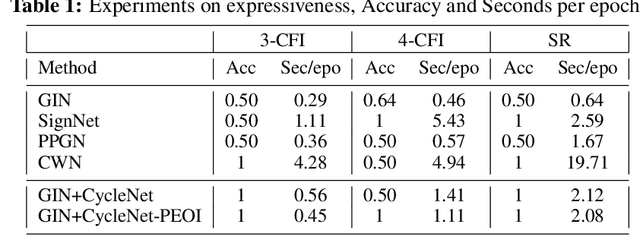
Cycles are fundamental elements in graph-structured data and have demonstrated their effectiveness in enhancing graph learning models. To encode such information into a graph learning framework, prior works often extract a summary quantity, ranging from the number of cycles to the more sophisticated persistence diagram summaries. However, more detailed information, such as which edges are encoded in a cycle, has not yet been used in graph neural networks. In this paper, we make one step towards addressing this gap, and propose a structure encoding module, called CycleNet, that encodes cycle information via edge structure encoding in a permutation invariant manner. To efficiently encode the space of all cycles, we start with a cycle basis (i.e., a minimal set of cycles generating the cycle space) which we compute via the kernel of the 1-dimensional Hodge Laplacian of the input graph. To guarantee the encoding is invariant w.r.t. the choice of cycle basis, we encode the cycle information via the orthogonal projector of the cycle basis, which is inspired by BasisNet proposed by Lim et al. We also develop a more efficient variant which however requires that the input graph has a unique shortest cycle basis. To demonstrate the effectiveness of the proposed module, we provide some theoretical understandings of its expressive power. Moreover, we show via a range of experiments that networks enhanced by our CycleNet module perform better in various benchmarks compared to several existing SOTA models.

Efficiently Counting Substructures by Subgraph GNNs without Running GNN on Subgraphs

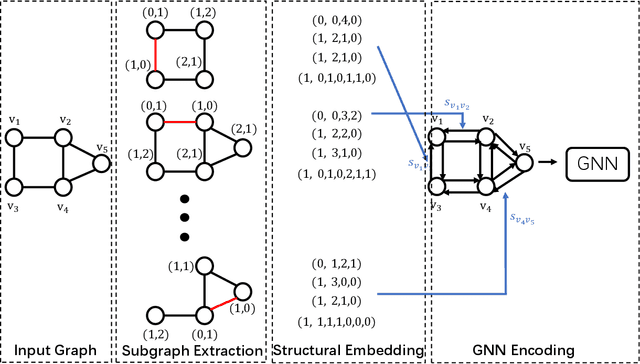
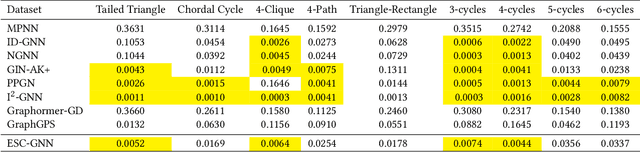
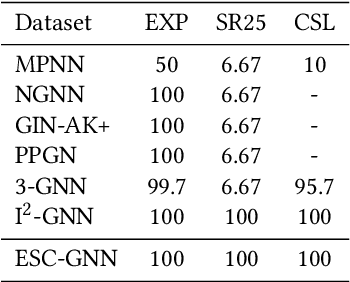
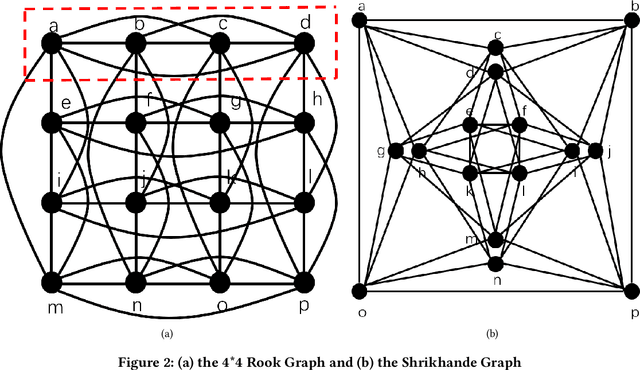
Using graph neural networks (GNNs) to approximate specific functions such as counting graph substructures is a recent trend in graph learning. Among these works, a popular way is to use subgraph GNNs, which decompose the input graph into a collection of subgraphs and enhance the representation of the graph by applying GNN to individual subgraphs. Although subgraph GNNs are able to count complicated substructures, they suffer from high computational and memory costs. In this paper, we address a non-trivial question: can we count substructures efficiently with GNNs? To answer the question, we first theoretically show that the distance to the rooted nodes within subgraphs is key to boosting the counting power of subgraph GNNs. We then encode such information into structural embeddings, and precompute the embeddings to avoid extracting information over all subgraphs via GNNs repeatedly. Experiments on various benchmarks show that the proposed model can preserve the counting power of subgraph GNNs while running orders of magnitude faster.

Neural Approximation of Extended Persistent Homology on Graphs

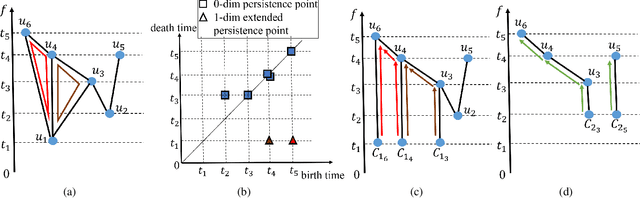
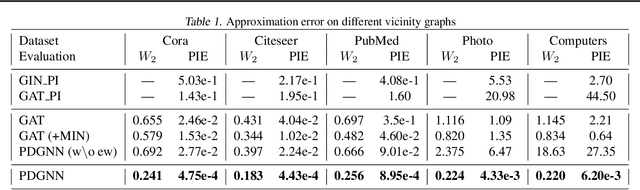
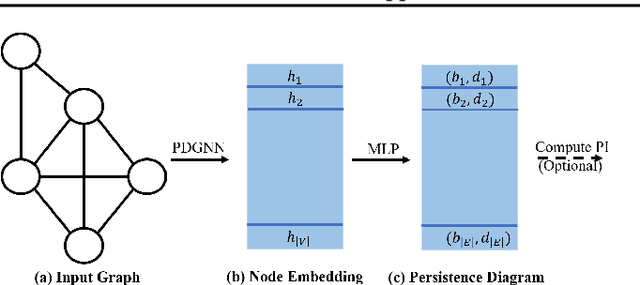
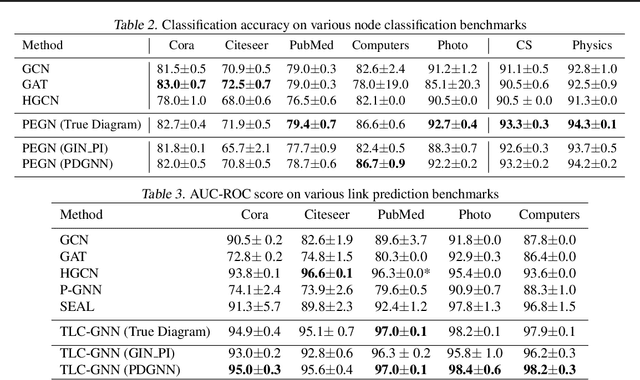
Persistent homology is a widely used theory in topological data analysis. In the context of graph learning, topological features based on persistent homology have been used to capture potentially high-order structural information so as to augment existing graph neural network methods. However, computing extended persistent homology summaries remains slow for large and dense graphs, especially since in learning applications one has to carry out this computation potentially many times. Inspired by recent success in neural algorithmic reasoning, we propose a novel learning method to compute extended persistence diagrams on graphs. The proposed neural network aims to simulate a specific algorithm and learns to compute extended persistence diagrams for new graphs efficiently. Experiments on approximating extended persistence diagrams and several downstream graph representation learning tasks demonstrate the effectiveness of our method. Our method is also efficient; on large and dense graphs, we accelerate the computation by nearly 100 times.

A Topological View of Rule Learning in Knowledge Graphs

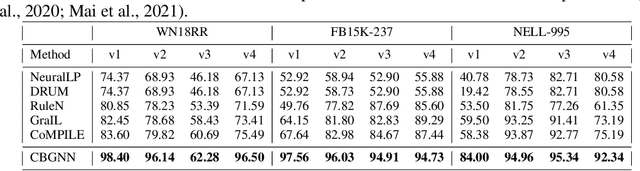
Inductive relation prediction is an important learning task for knowledge graph completion. One can use the existence of rules, namely a sequence of relations, to predict the relation between two entities. Previous works view rules as paths and primarily focus on the searching of paths between entities. The space of paths is huge, and one has to sacrifice either efficiency or accuracy. In this paper, we consider rules in knowledge graphs as cycles and show that the space of cycles has a unique structure based on the theory of algebraic topology. By exploring the linear structure of the cycle space, we can improve the searching efficiency of rules. We propose to collect cycle bases that span the space of cycles. We build a novel GNN framework on the collected cycles to learn the representations of cycles, and to predict the existence/non-existence of a relation. Our method achieves state-of-the-art performance on benchmarks.

Handwritten Mathematical Expression Recognition with Bidirectionally Trained Transformer

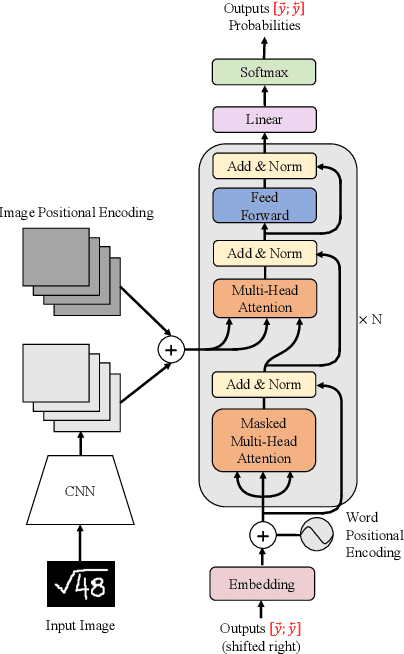
Encoder-decoder models have made great progress on handwritten mathematical expression recognition recently. However, it is still a challenge for existing methods to assign attention to image features accurately. Moreover, those encoder-decoder models usually adopt RNN-based models in their decoder part, which makes them inefficient in processing long $\LaTeX{}$ sequences. In this paper, a transformer-based decoder is employed to replace RNN-based ones, which makes the whole model architecture very concise. Furthermore, a novel training strategy is introduced to fully exploit the potential of the transformer in bidirectional language modeling. Compared to several methods that do not use data augmentation, experiments demonstrate that our model improves the ExpRate of current state-of-the-art methods on CROHME 2014 by 2.23%. Similarly, on CROHME 2016 and CROHME 2019, we improve the ExpRate by 1.92% and 2.28% respectively.

Automatic Description Construction for Math Expression via Topic Relation Graph

Math expressions are important parts of scientific and educational documents, but some of them may be challenging for junior scholars or students to understand. Nevertheless, constructing textual descriptions for math expressions is nontrivial. In this paper, we explore the feasibility to automatically construct descriptions for math expressions. But there are two challenges that need to be addressed: 1) finding relevant documents since a math equation understanding usually requires several topics, but these topics are often explained in different documents. 2) the sparsity of the collected relevant documents making it difficult to extract reasonable descriptions. Different documents mainly focus on different topics which makes model hard to extract salient information and organize them to form a description of math expressions. To address these issues, we propose a hybrid model (MathDes) which contains two important modules: Selector and Summarizer. In the Selector, a Topic Relation Graph (TRG) is proposed to obtain the relevant documents which contain the comprehensive information of math expressions. TRG is a graph built according to the citations between expressions. In the Summarizer, a summarization model under the Integer Linear Programming (ILP) framework is proposed. This module constructs the final description with the help of a timeline that is extracted from TRG. The experimental results demonstrate that our methods are promising for this task and outperform the baselines in all aspects.

Persistence Homology for Link Prediction: An Interactive View

Link prediction is an important learning task for graph-structured data. In this paper, we propose a novel topological approach to characterize interactions between two nodes. Our topological feature, based on the extended persistence homology, encodes rich structural information regarding the multi-hop paths connecting nodes. Based on this feature, we propose a graph neural network method that outperforms state-of-the-arts on different benchmarks. As another contribution, we propose a novel algorithm to more efficiently compute the extended persistent diagrams for graphs. This algorithm can be generally applied to accelerate many other topological methods for graph learning tasks.

ConvMath: A Convolutional Sequence Network for Mathematical Expression Recognition

Despite the recent advances in optical character recognition (OCR), mathematical expressions still face a great challenge to recognize due to their two-dimensional graphical layout. In this paper, we propose a convolutional sequence modeling network, ConvMath, which converts the mathematical expression description in an image into a LaTeX sequence in an end-to-end way. The network combines an image encoder for feature extraction and a convolutional decoder for sequence generation. Compared with other Long Short Term Memory(LSTM) based encoder-decoder models, ConvMath is entirely based on convolution, thus it is easy to perform parallel computation. Besides, the network adopts multi-layer attention mechanism in the decoder, which allows the model to align output symbols with source feature vectors automatically, and alleviates the problem of lacking coverage while training the model. The performance of ConvMath is evaluated on an open dataset named IM2LATEX-100K, including 103556 samples. The experimental results demonstrate that the proposed network achieves state-of-the-art accuracy and much better efficiency than previous methods.