Neural Approximation of Extended Persistent Homology on Graphs

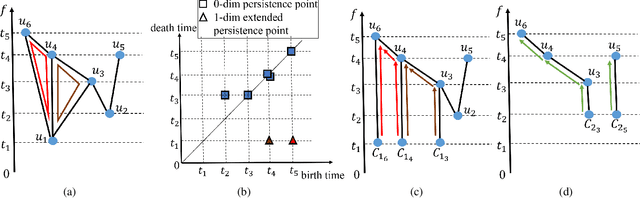
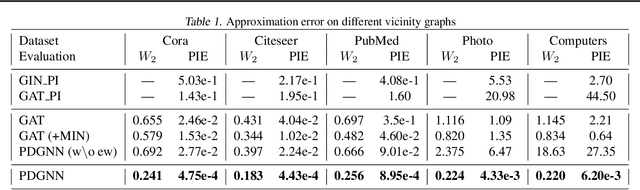
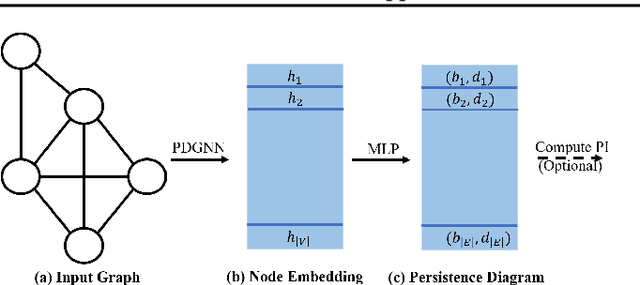
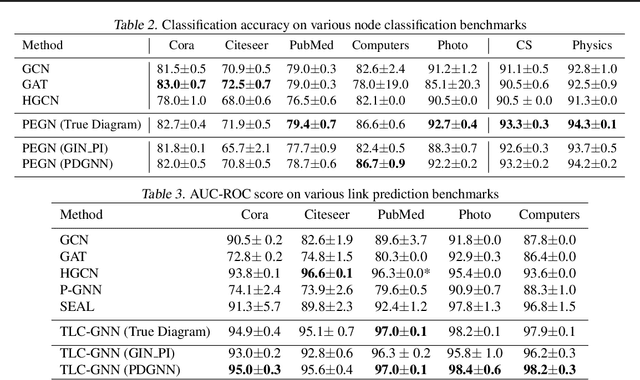
Persistent homology is a widely used theory in topological data analysis. In the context of graph learning, topological features based on persistent homology have been used to capture potentially high-order structural information so as to augment existing graph neural network methods. However, computing extended persistent homology summaries remains slow for large and dense graphs, especially since in learning applications one has to carry out this computation potentially many times. Inspired by recent success in neural algorithmic reasoning, we propose a novel learning method to compute extended persistence diagrams on graphs. The proposed neural network aims to simulate a specific algorithm and learns to compute extended persistence diagrams for new graphs efficiently. Experiments on approximating extended persistence diagrams and several downstream graph representation learning tasks demonstrate the effectiveness of our method. Our method is also efficient; on large and dense graphs, we accelerate the computation by nearly 100 times.