A Topological View of Rule Learning in Knowledge Graphs
Paper and Code
Oct 06, 2021


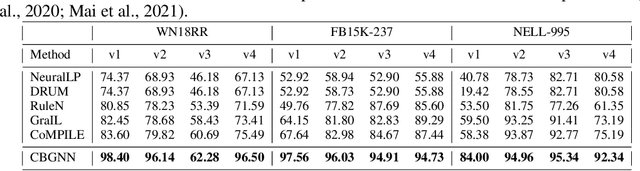
Inductive relation prediction is an important learning task for knowledge graph completion. One can use the existence of rules, namely a sequence of relations, to predict the relation between two entities. Previous works view rules as paths and primarily focus on the searching of paths between entities. The space of paths is huge, and one has to sacrifice either efficiency or accuracy. In this paper, we consider rules in knowledge graphs as cycles and show that the space of cycles has a unique structure based on the theory of algebraic topology. By exploring the linear structure of the cycle space, we can improve the searching efficiency of rules. We propose to collect cycle bases that span the space of cycles. We build a novel GNN framework on the collected cycles to learn the representations of cycles, and to predict the existence/non-existence of a relation. Our method achieves state-of-the-art performance on benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge