Efficiently Counting Substructures by Subgraph GNNs without Running GNN on Subgraphs
Paper and Code
Mar 19, 2023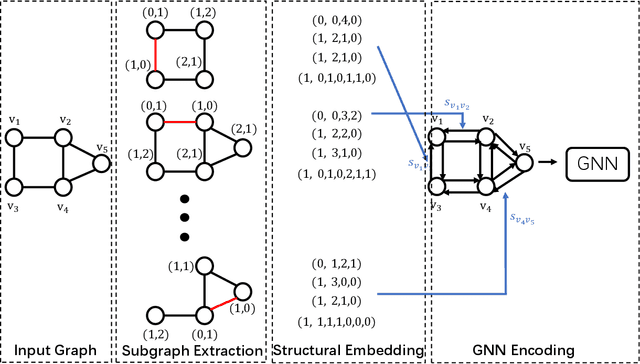
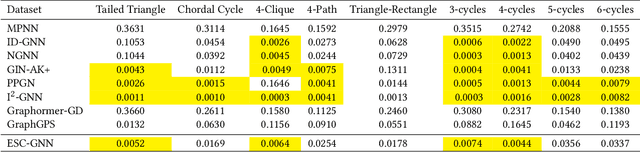
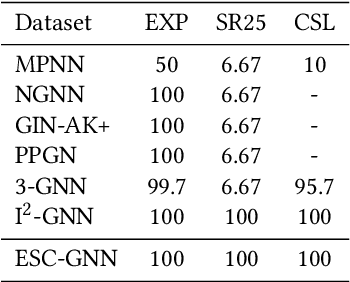
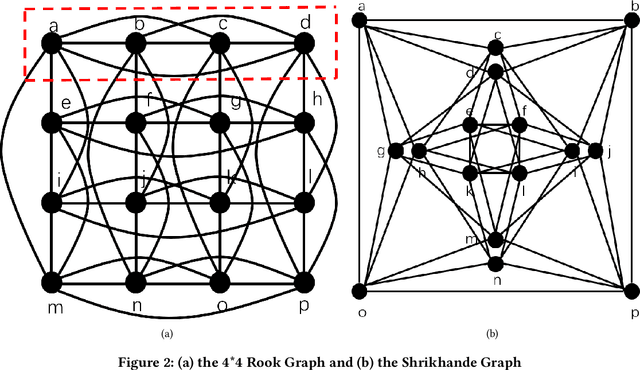
Using graph neural networks (GNNs) to approximate specific functions such as counting graph substructures is a recent trend in graph learning. Among these works, a popular way is to use subgraph GNNs, which decompose the input graph into a collection of subgraphs and enhance the representation of the graph by applying GNN to individual subgraphs. Although subgraph GNNs are able to count complicated substructures, they suffer from high computational and memory costs. In this paper, we address a non-trivial question: can we count substructures efficiently with GNNs? To answer the question, we first theoretically show that the distance to the rooted nodes within subgraphs is key to boosting the counting power of subgraph GNNs. We then encode such information into structural embeddings, and precompute the embeddings to avoid extracting information over all subgraphs via GNNs repeatedly. Experiments on various benchmarks show that the proposed model can preserve the counting power of subgraph GNNs while running orders of magnitude faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge