Cycle Invariant Positional Encoding for Graph Representation Learning
Paper and Code
Nov 30, 2023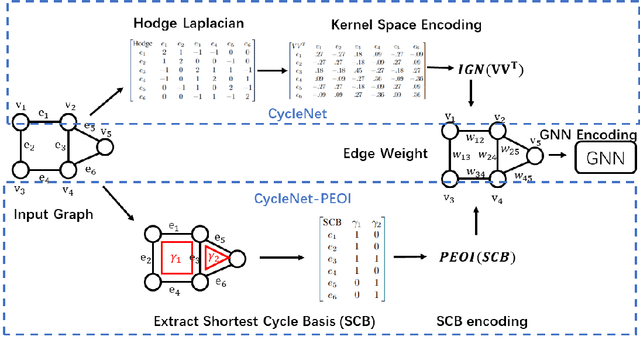
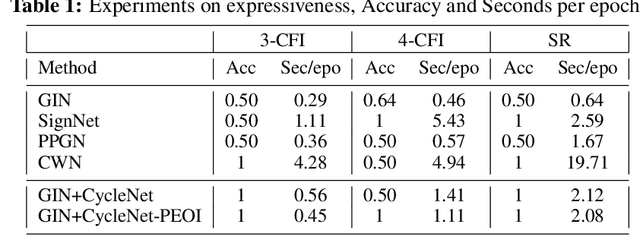

Cycles are fundamental elements in graph-structured data and have demonstrated their effectiveness in enhancing graph learning models. To encode such information into a graph learning framework, prior works often extract a summary quantity, ranging from the number of cycles to the more sophisticated persistence diagram summaries. However, more detailed information, such as which edges are encoded in a cycle, has not yet been used in graph neural networks. In this paper, we make one step towards addressing this gap, and propose a structure encoding module, called CycleNet, that encodes cycle information via edge structure encoding in a permutation invariant manner. To efficiently encode the space of all cycles, we start with a cycle basis (i.e., a minimal set of cycles generating the cycle space) which we compute via the kernel of the 1-dimensional Hodge Laplacian of the input graph. To guarantee the encoding is invariant w.r.t. the choice of cycle basis, we encode the cycle information via the orthogonal projector of the cycle basis, which is inspired by BasisNet proposed by Lim et al. We also develop a more efficient variant which however requires that the input graph has a unique shortest cycle basis. To demonstrate the effectiveness of the proposed module, we provide some theoretical understandings of its expressive power. Moreover, we show via a range of experiments that networks enhanced by our CycleNet module perform better in various benchmarks compared to several existing SOTA models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge