A Constrained Optimization Approach to Bilevel Optimization with Multiple Inner Minima

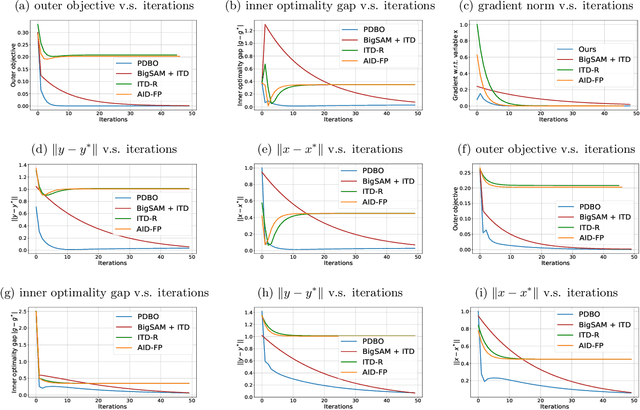
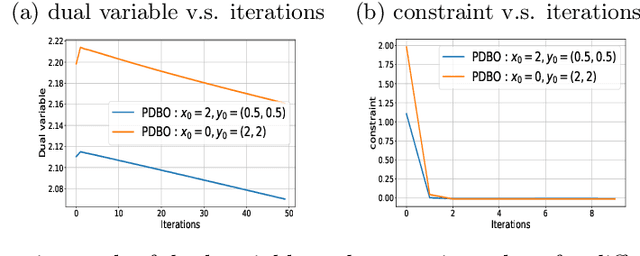
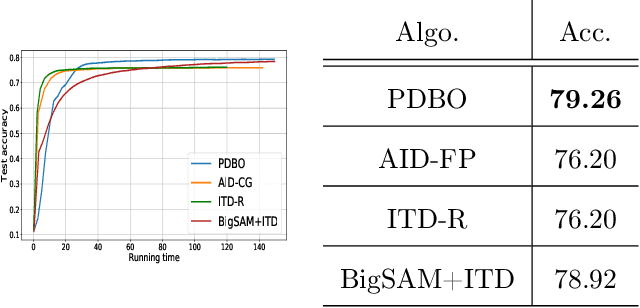
Bilevel optimization has found extensive applications in modern machine learning problems such as hyperparameter optimization, neural architecture search, meta-learning, etc. While bilevel problems with a unique inner minimal point (e.g., where the inner function is strongly convex) are well understood, bilevel problems with multiple inner minimal points remains to be a challenging and open problem. Existing algorithms designed for such a problem were applicable to restricted situations and do not come with the full guarantee of convergence. In this paper, we propose a new approach, which convert the bilevel problem to an equivalent constrained optimization, and then the primal-dual algorithm can be used to solve the problem. Such an approach enjoys a few advantages including (a) addresses the multiple inner minima challenge; (b) features fully first-order efficiency without involving second-order Hessian and Jacobian computations, as opposed to most existing gradient-based bilevel algorithms; (c) admits the convergence guarantee via constrained nonconvex optimization. Our experiments further demonstrate the desired performance of the proposed approach.

Faster Algorithm and Sharper Analysis for Constrained Markov Decision Process

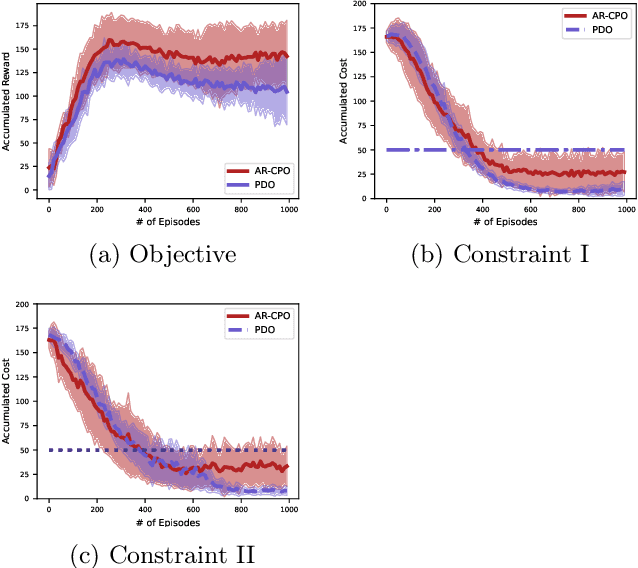
The problem of constrained Markov decision process (CMDP) is investigated, where an agent aims to maximize the expected accumulated discounted reward subject to multiple constraints on its utilities/costs. A new primal-dual approach is proposed with a novel integration of three ingredients: entropy regularized policy optimizer, dual variable regularizer, and Nesterov's accelerated gradient descent dual optimizer, all of which are critical to achieve a faster convergence. The finite-time error bound of the proposed approach is characterized. Despite the challenge of the nonconcave objective subject to nonconcave constraints, the proposed approach is shown to converge to the global optimum with a complexity of $\tilde{\mathcal O}(1/\epsilon)$ in terms of the optimality gap and the constraint violation, which improves the complexity of the existing primal-dual approach by a factor of $\mathcal O(1/\epsilon)$ \citep{ding2020natural,paternain2019constrained}. This is the first demonstration that nonconcave CMDP problems can attain the complexity lower bound of $\mathcal O(1/\epsilon)$ for convex optimization subject to convex constraints. Our primal-dual approach and non-asymptotic analysis are agnostic to the RL optimizer used, and thus are more flexible for practical applications. More generally, our approach also serves as the first algorithm that provably accelerates constrained nonconvex optimization with zero duality gap by exploiting the geometries such as the gradient dominance condition, for which the existing acceleration methods for constrained convex optimization are not applicable.

PER-ETD: A Polynomially Efficient Emphatic Temporal Difference Learning Method

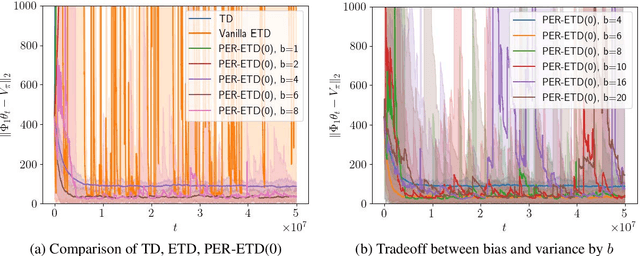
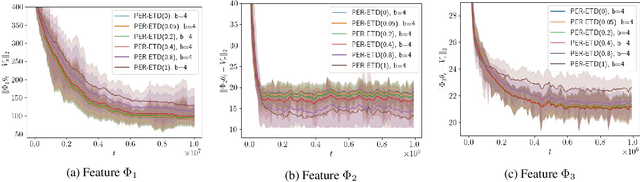
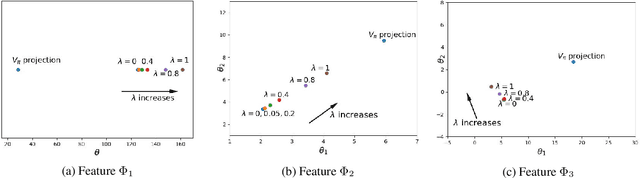
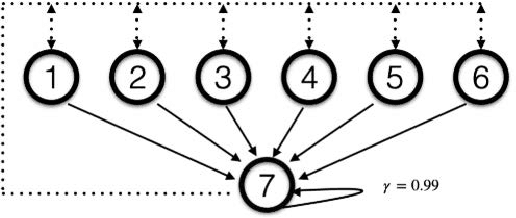
Emphatic temporal difference (ETD) learning (Sutton et al., 2016) is a successful method to conduct the off-policy value function evaluation with function approximation. Although ETD has been shown to converge asymptotically to a desirable value function, it is well-known that ETD often encounters a large variance so that its sample complexity can increase exponentially fast with the number of iterations. In this work, we propose a new ETD method, called PER-ETD (i.e., PEriodically Restarted-ETD), which restarts and updates the follow-on trace only for a finite period for each iteration of the evaluation parameter. Further, PER-ETD features a design of the logarithmical increase of the restart period with the number of iterations, which guarantees the best trade-off between the variance and bias and keeps both vanishing sublinearly. We show that PER-ETD converges to the same desirable fixed point as ETD, but improves the exponential sample complexity of ETD to be polynomials. Our experiments validate the superior performance of PER-ETD and its advantage over ETD.

When Will Generative Adversarial Imitation Learning Algorithms Attain Global Convergence

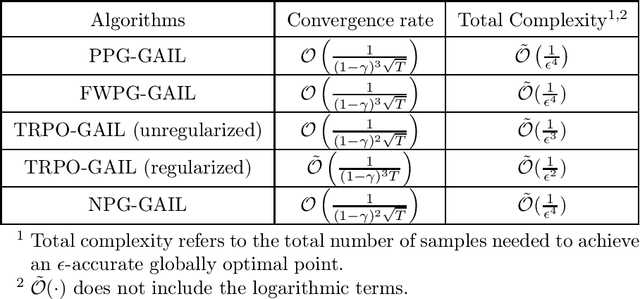
Generative adversarial imitation learning (GAIL) is a popular inverse reinforcement learning approach for jointly optimizing policy and reward from expert trajectories. A primary question about GAIL is whether applying a certain policy gradient algorithm to GAIL attains a global minimizer (i.e., yields the expert policy), for which existing understanding is very limited. Such global convergence has been shown only for the linear (or linear-type) MDP and linear (or linearizable) reward. In this paper, we study GAIL under general MDP and for nonlinear reward function classes (as long as the objective function is strongly concave with respect to the reward parameter). We characterize the global convergence with a sublinear rate for a broad range of commonly used policy gradient algorithms, all of which are implemented in an alternating manner with stochastic gradient ascent for reward update, including projected policy gradient (PPG)-GAIL, Frank-Wolfe policy gradient (FWPG)-GAIL, trust region policy optimization (TRPO)-GAIL and natural policy gradient (NPG)-GAIL. This is the first systematic theoretical study of GAIL for global convergence.

Robust Stochastic Bandit Algorithms under Probabilistic Unbounded Adversarial Attack

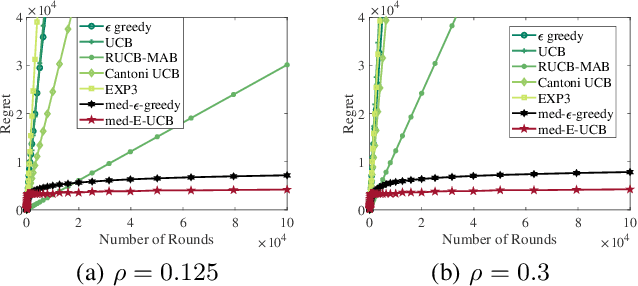
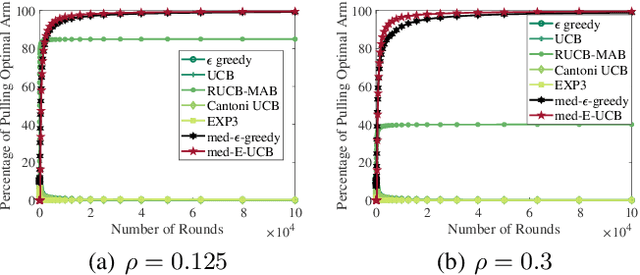
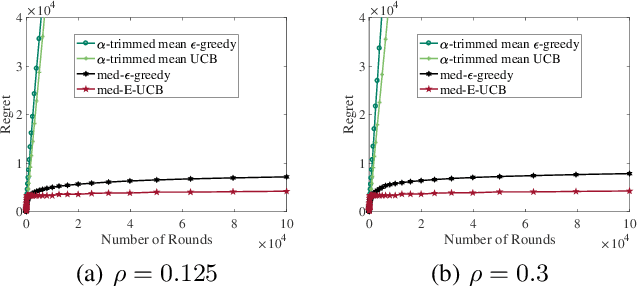
The multi-armed bandit formalism has been extensively studied under various attack models, in which an adversary can modify the reward revealed to the player. Previous studies focused on scenarios where the attack value either is bounded at each round or has a vanishing probability of occurrence. These models do not capture powerful adversaries that can catastrophically perturb the revealed reward. This paper investigates the attack model where an adversary attacks with a certain probability at each round, and its attack value can be arbitrary and unbounded if it attacks. Furthermore, the attack value does not necessarily follow a statistical distribution. We propose a novel sample median-based and exploration-aided UCB algorithm (called med-E-UCB) and a median-based $\epsilon$-greedy algorithm (called med-$\epsilon$-greedy). Both of these algorithms are provably robust to the aforementioned attack model. More specifically we show that both algorithms achieve $\mathcal{O}(\log T)$ pseudo-regret (i.e., the optimal regret without attacks). We also provide a high probability guarantee of $\mathcal{O}(\log T)$ regret with respect to random rewards and random occurrence of attacks. These bounds are achieved under arbitrary and unbounded reward perturbation as long as the attack probability does not exceed a certain constant threshold. We provide multiple synthetic simulations of the proposed algorithms to verify these claims and showcase the inability of existing techniques to achieve sublinear regret. We also provide experimental results of the algorithm operating in a cognitive radio setting using multiple software-defined radios.