PER-ETD: A Polynomially Efficient Emphatic Temporal Difference Learning Method
Paper and Code
Oct 13, 2021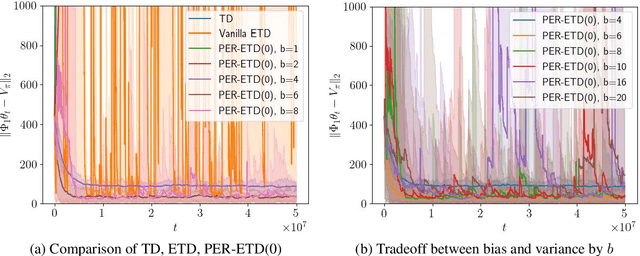
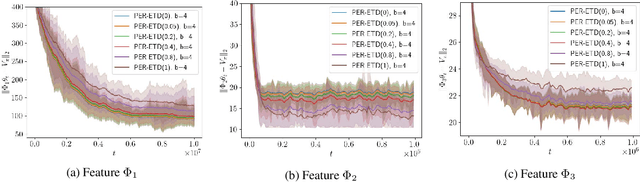
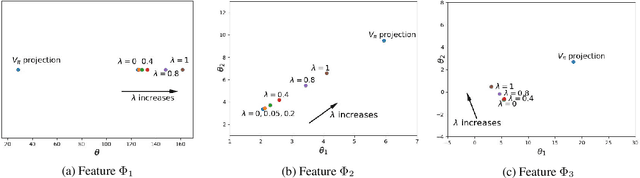
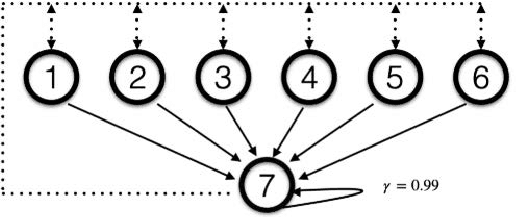
Emphatic temporal difference (ETD) learning (Sutton et al., 2016) is a successful method to conduct the off-policy value function evaluation with function approximation. Although ETD has been shown to converge asymptotically to a desirable value function, it is well-known that ETD often encounters a large variance so that its sample complexity can increase exponentially fast with the number of iterations. In this work, we propose a new ETD method, called PER-ETD (i.e., PEriodically Restarted-ETD), which restarts and updates the follow-on trace only for a finite period for each iteration of the evaluation parameter. Further, PER-ETD features a design of the logarithmical increase of the restart period with the number of iterations, which guarantees the best trade-off between the variance and bias and keeps both vanishing sublinearly. We show that PER-ETD converges to the same desirable fixed point as ETD, but improves the exponential sample complexity of ETD to be polynomials. Our experiments validate the superior performance of PER-ETD and its advantage over ETD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge