A Constrained Optimization Approach to Bilevel Optimization with Multiple Inner Minima
Paper and Code
Mar 01, 2022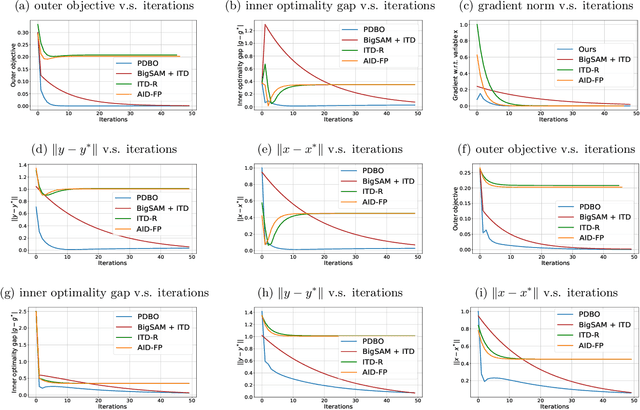
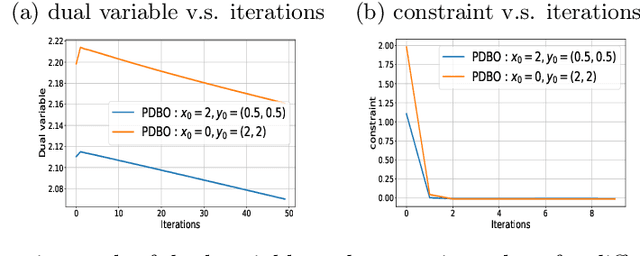
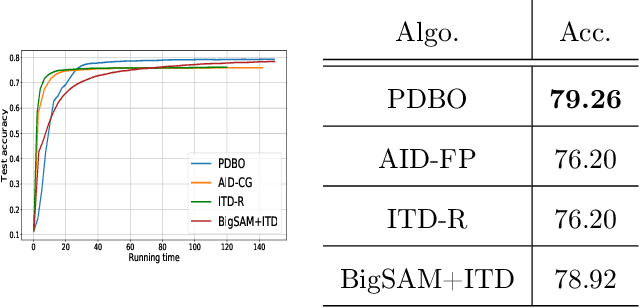
Bilevel optimization has found extensive applications in modern machine learning problems such as hyperparameter optimization, neural architecture search, meta-learning, etc. While bilevel problems with a unique inner minimal point (e.g., where the inner function is strongly convex) are well understood, bilevel problems with multiple inner minimal points remains to be a challenging and open problem. Existing algorithms designed for such a problem were applicable to restricted situations and do not come with the full guarantee of convergence. In this paper, we propose a new approach, which convert the bilevel problem to an equivalent constrained optimization, and then the primal-dual algorithm can be used to solve the problem. Such an approach enjoys a few advantages including (a) addresses the multiple inner minima challenge; (b) features fully first-order efficiency without involving second-order Hessian and Jacobian computations, as opposed to most existing gradient-based bilevel algorithms; (c) admits the convergence guarantee via constrained nonconvex optimization. Our experiments further demonstrate the desired performance of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge