HyperZero: A Customized End-to-End Auto-Tuning System for Recommendation with Hourly Feedback

Modern recommendation systems can be broadly divided into two key stages: the ranking stage, where the system predicts various user engagements (e.g., click-through rate, like rate, follow rate, watch time), and the value model stage, which aggregates these predictive scores through a function (e.g., a linear combination defined by a weight vector) to measure the value of each content by a single numerical score. Both stages play roughly equally important roles in real industrial systems; however, how to optimize the model weights for the second stage still lacks systematic study. This paper focuses on optimizing the second stage through auto-tuning technology. Although general auto-tuning systems and solutions - both from established production practices and open-source solutions - can address this problem, they typically require weeks or even months to identify a feasible solution. Such prolonged tuning processes are unacceptable in production environments for recommendation systems, as suboptimal value models can severely degrade user experience. An effective auto-tuning solution is required to identify a viable model within 2-3 days, rather than the extended timelines typically associated with existing approaches. In this paper, we introduce a practical auto-tuning system named HyperZero that addresses these time constraints while effectively solving the unique challenges inherent in modern recommendation systems. Moreover, this framework has the potential to be expanded to broader tuning tasks within recommendation systems.

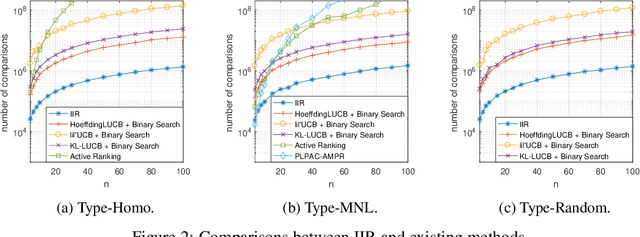
The Sample Complexity of Best-$k$ Items Selection from Pairwise Comparisons

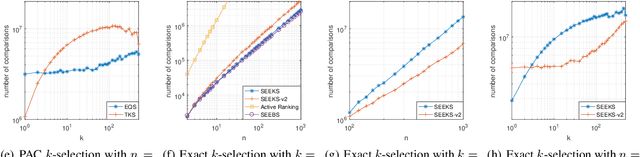
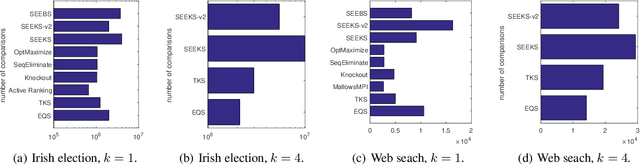
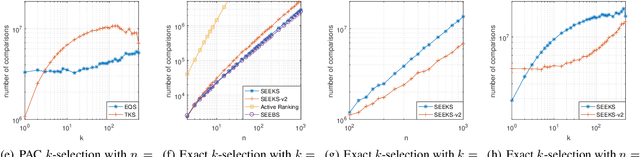
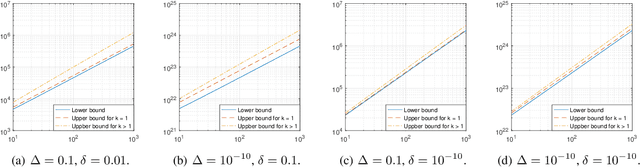
This paper studies the sample complexity (aka number of comparisons) bounds for the active best-$k$ items selection from pairwise comparisons. From a given set of items, the learner can make pairwise comparisons on every pair of items, and each comparison returns an independent noisy result about the preferred item. At any time, the learner can adaptively choose a pair of items to compare according to past observations (i.e., active learning). The learner's goal is to find the (approximately) best-$k$ items with a given confidence, while trying to use as few comparisons as possible. In this paper, we study two problems: (i) finding the probably approximately correct (PAC) best-$k$ items and (ii) finding the exact best-$k$ items, both under strong stochastic transitivity and stochastic triangle inequality. For PAC best-$k$ items selection, we first show a lower bound and then propose an algorithm whose sample complexity upper bound matches the lower bound up to a constant factor. For the exact best-$k$ items selection, we first prove a worst-instance lower bound. We then propose two algorithms based on our PAC best items selection algorithms: one works for $k=1$ and is sample complexity optimal up to a loglog factor, and the other works for all values of $k$ and is sample complexity optimal up to a log factor.

Multi-Armed Bandits with Local Differential Privacy

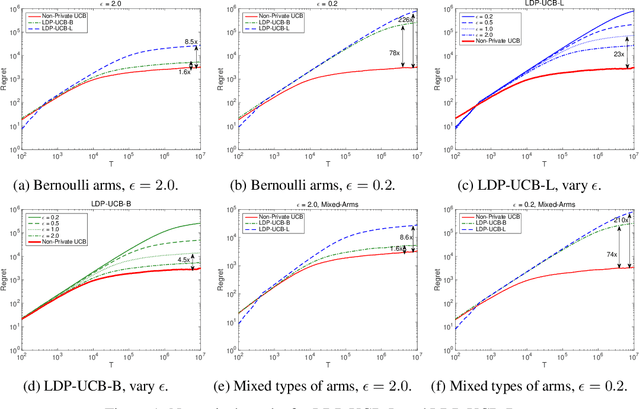
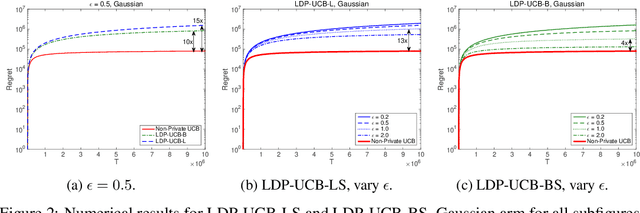
This paper investigates the problem of regret minimization for multi-armed bandit (MAB) problems with local differential privacy (LDP) guarantee. In stochastic bandit systems, the rewards may refer to the users' activities, which may involve private information and the users may not want the agent to know. However, in many cases, the agent needs to know these activities to provide better services such as recommendations and news feeds. To handle this dilemma, we adopt differential privacy and study the regret upper and lower bounds for MAB algorithms with a given LDP guarantee. In this paper, we prove a lower bound and propose algorithms whose regret upper bounds match the lower bound up to constant factors. Numerical experiments also confirm our conclusions.

On Sample Complexity Upper and Lower Bounds for Exact Ranking from Noisy Comparisons

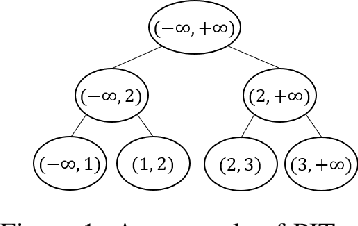
This paper studies the problem of finding the exact ranking from noisy comparisons. A comparison over a set of $m$ items produces a noisy outcome about the most preferred item, and reveals some information about the ranking. By repeatedly and adaptively choosing items to compare, we want to fully rank the items with a certain confidence, and use as few comparisons as possible. Different from most previous works, in this paper, we have three main novelties: (i) compared to prior works, our upper bounds (algorithms) and lower bounds on the sample complexity (aka number of comparisons) require the minimal assumptions on the instances, and are not restricted to specific models; (ii) we give lower bounds and upper bounds on instances with unequal noise levels; and (iii) this paper aims at the exact ranking without knowledge on the instances, while most of the previous works either focus on approximate rankings or study exact ranking but require prior knowledge. We first derive lower bounds for pairwise ranking (i.e., compare two items each time), and then propose (nearly) optimal pairwise ranking algorithms. We further make extensions to listwise ranking (i.e., comparing multiple items each time). Numerical results also show our improvements against the state of the art.

Exploring $k$ out of Top $ρ$ Fraction of Arms in Stochastic Bandits

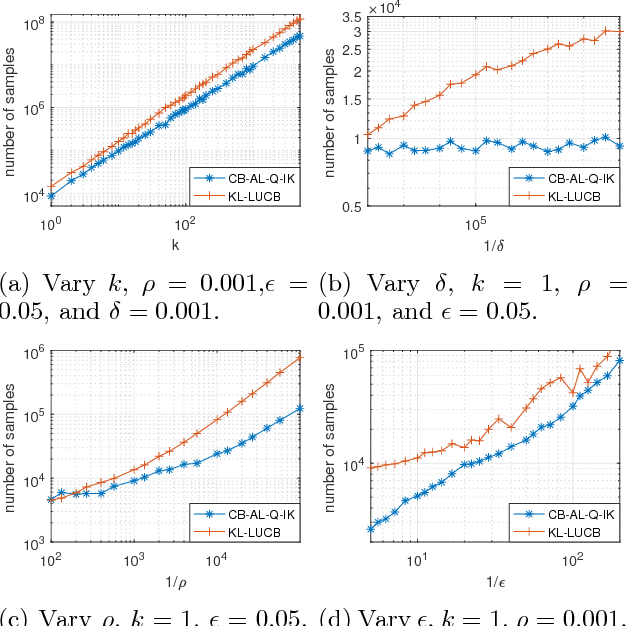
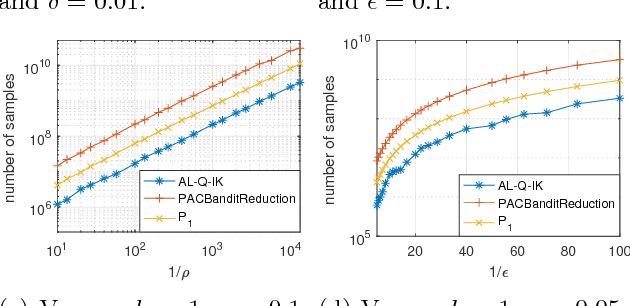
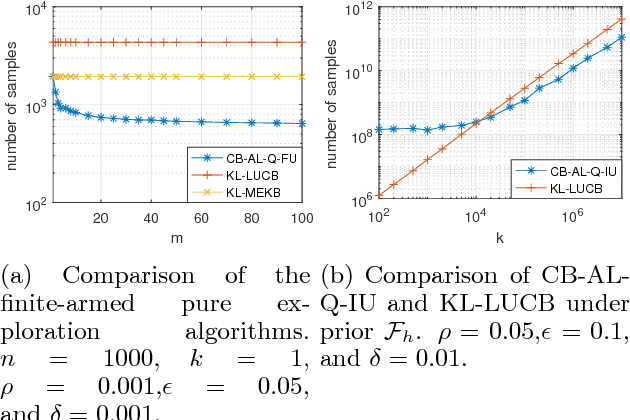
This paper studies the problem of identifying any $k$ distinct arms among the top $\rho$ fraction (e.g., top 5\%) of arms from a finite or infinite set with a probably approximately correct (PAC) tolerance $\epsilon$. We consider two cases: (i) when the threshold of the top arms' expected rewards is known and (ii) when it is unknown. We prove lower bounds for the four variants (finite or infinite, and threshold known or unknown), and propose algorithms for each. Two of these algorithms are shown to be sample complexity optimal (up to constant factors) and the other two are optimal up to a log factor. Results in this paper provide up to $\rho n/k$ reductions compared with the "$k$-exploration" algorithms that focus on finding the (PAC) best $k$ arms out of $n$ arms. We also numerically show improvements over the state-of-the-art.

PAC Ranking from Pairwise and Listwise Queries: Lower Bounds and Upper Bounds

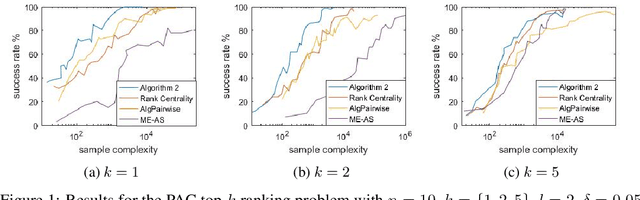
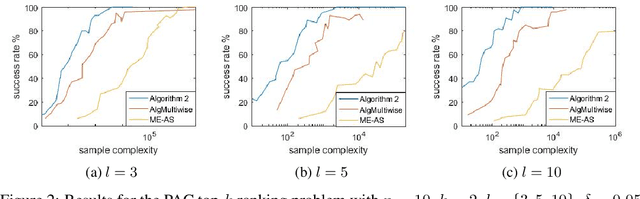
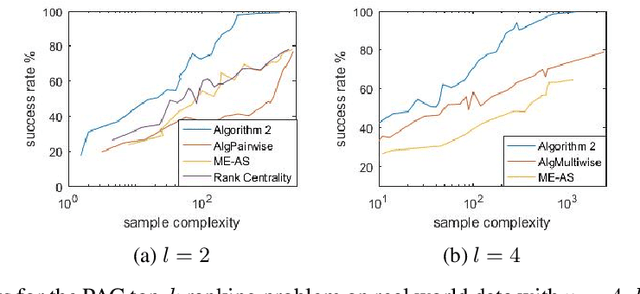
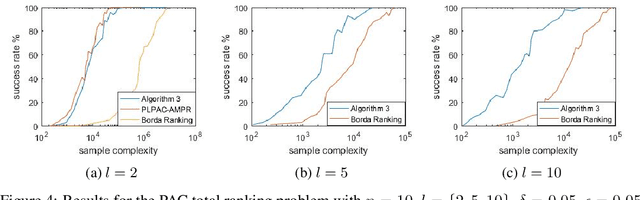
This paper explores the adaptive (active) PAC (probably approximately correct) top-$k$ ranking (i.e., top-$k$ item selection) and total ranking problems from $l$-wise ($l\geq 2$) comparisons under the multinomial logit (MNL) model. By adaptively choosing sets to query and observing the noisy output of the most favored item of each query, we want to design ranking algorithms that recover the top-$k$ or total ranking using as few queries as possible. For the PAC top-$k$ ranking problem, we derive a lower bound on the sample complexity (aka number of queries), and propose an algorithm that is sample-complexity-optimal up to an $O(\log(k+l)/\log{k})$ factor. When $l=2$ (i.e., pairwise comparisons) or $l=O(poly(k))$, this algorithm matches the lower bound. For the PAC total ranking problem, we derive a tight lower bound, and propose an algorithm that matches the lower bound. When $l=2$, the MNL model reduces to the popular Plackett-Luce (PL) model. In this setting, our results still outperform the state-of-the-art both theoretically and numerically. We also compare our algorithms with the state-of-the-art using synthetic data as well as real-world data to verify the efficiency of our algorithms.