Multi-Armed Bandits with Local Differential Privacy
Paper and Code
Jul 06, 2020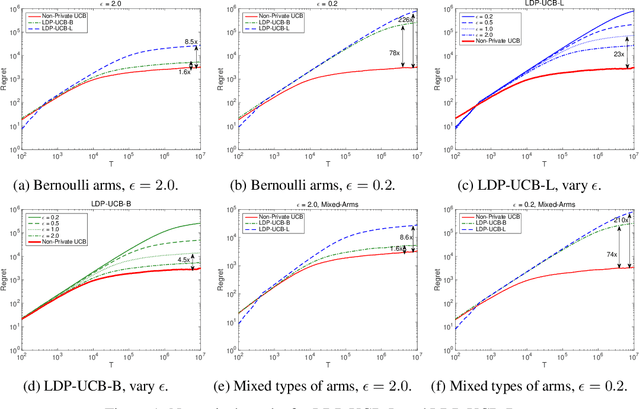
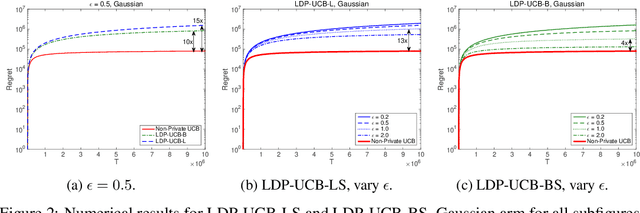
This paper investigates the problem of regret minimization for multi-armed bandit (MAB) problems with local differential privacy (LDP) guarantee. In stochastic bandit systems, the rewards may refer to the users' activities, which may involve private information and the users may not want the agent to know. However, in many cases, the agent needs to know these activities to provide better services such as recommendations and news feeds. To handle this dilemma, we adopt differential privacy and study the regret upper and lower bounds for MAB algorithms with a given LDP guarantee. In this paper, we prove a lower bound and propose algorithms whose regret upper bounds match the lower bound up to constant factors. Numerical experiments also confirm our conclusions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge