PAC Ranking from Pairwise and Listwise Queries: Lower Bounds and Upper Bounds
Paper and Code
Sep 10, 2018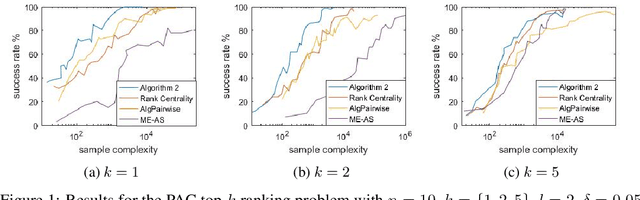
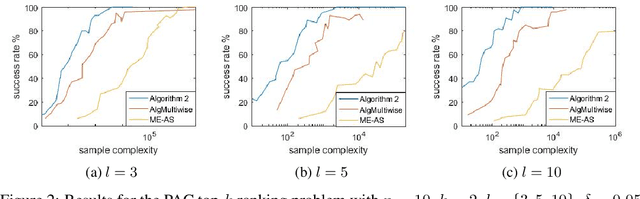
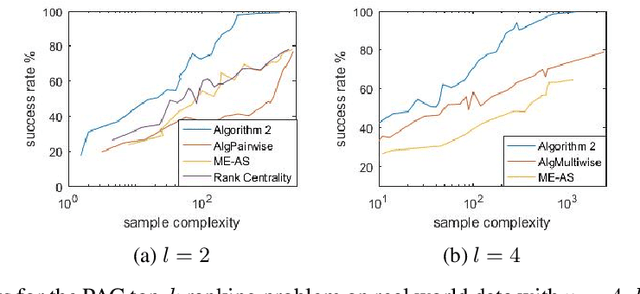
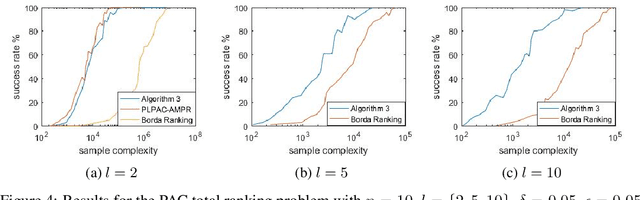
This paper explores the adaptive (active) PAC (probably approximately correct) top-$k$ ranking (i.e., top-$k$ item selection) and total ranking problems from $l$-wise ($l\geq 2$) comparisons under the multinomial logit (MNL) model. By adaptively choosing sets to query and observing the noisy output of the most favored item of each query, we want to design ranking algorithms that recover the top-$k$ or total ranking using as few queries as possible. For the PAC top-$k$ ranking problem, we derive a lower bound on the sample complexity (aka number of queries), and propose an algorithm that is sample-complexity-optimal up to an $O(\log(k+l)/\log{k})$ factor. When $l=2$ (i.e., pairwise comparisons) or $l=O(poly(k))$, this algorithm matches the lower bound. For the PAC total ranking problem, we derive a tight lower bound, and propose an algorithm that matches the lower bound. When $l=2$, the MNL model reduces to the popular Plackett-Luce (PL) model. In this setting, our results still outperform the state-of-the-art both theoretically and numerically. We also compare our algorithms with the state-of-the-art using synthetic data as well as real-world data to verify the efficiency of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge