Proximal Action Replacement for Behavior Cloning Actor-Critic in Offline Reinforcement Learning

Offline reinforcement learning (RL) optimizes policies from a previously collected static dataset and is an important branch of RL. A popular and promising approach is to regularize actor-critic methods with behavior cloning (BC), which yields realistic policies and mitigates bias from out-of-distribution actions, but can impose an often-overlooked performance ceiling: when dataset actions are suboptimal, indiscriminate imitation structurally prevents the actor from fully exploiting high-value regions suggested by the critic, especially in later training when imitation is already dominant. We formally analyzed this limitation by investigating convergence properties of BC-regularized actor-critic optimization and verified it on a controlled continuous bandit task. To break this ceiling, we propose proximal action replacement (PAR), a plug-and-play training sample replacer that progressively replaces low-value actions with high-value actions generated by a stable actor, broadening the action exploration space while reducing the impact of low-value data. PAR is compatible with multiple BC regularization paradigms. Extensive experiments across offline RL benchmarks show that PAR consistently improves performance and approaches state-of-the-art when combined with the basic TD3+BC.

Interference Factors and Compensation Methods when Using Infrared Thermography for Temperature Measurement: A Review

Infrared thermography (IRT) is a widely used temperature measurement technology, but it faces the problem of measurement errors under interference factors. This paper attempts to summarize the common interference factors and temperature compensation methods when applying IRT. According to the source of factors affecting the infrared temperature measurement accuracy, the interference factors are divided into three categories: factors from the external environment, factors from the measured object, and factors from the infrared thermal imager itself. At the same time, the existing compensation methods are classified into three categories: Mechanism Modeling based Compensation method (MMC), Data-Driven Compensation method (DDC), and Mechanism and Data jointly driven Compensation method (MDC). Furthermore, we discuss the problems existing in the temperature compensation methods and future research directions, aiming to provide some references for researchers in academia and industry when using IRT technology for temperature measurement.

Combining Priors with Experience: Confidence Calibration Based on Binomial Process Modeling

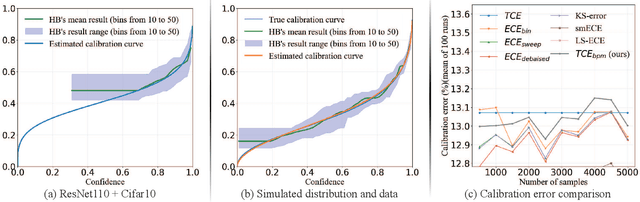
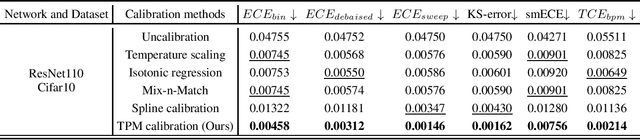
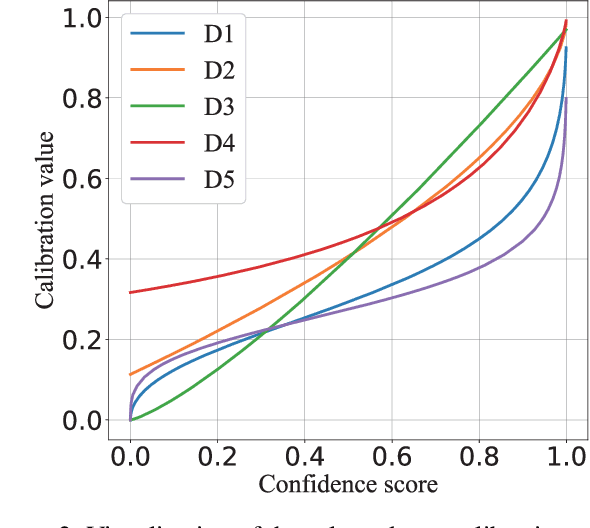
Confidence calibration of classification models is a technique to estimate the true posterior probability of the predicted class, which is critical for ensuring reliable decision-making in practical applications. Existing confidence calibration methods mostly use statistical techniques to estimate the calibration curve from data or fit a user-defined calibration function, but often overlook fully mining and utilizing the prior distribution behind the calibration curve. However, a well-informed prior distribution can provide valuable insights beyond the empirical data under the limited data or low-density regions of confidence scores. To fill this gap, this paper proposes a new method that integrates the prior distribution behind the calibration curve with empirical data to estimate a continuous calibration curve, which is realized by modeling the sampling process of calibration data as a binomial process and maximizing the likelihood function of the binomial process. We prove that the calibration curve estimating method is Lipschitz continuous with respect to data distribution and requires a sample size of $3/B$ of that required for histogram binning, where $B$ represents the number of bins. Also, a new calibration metric ($TCE_{bpm}$), which leverages the estimated calibration curve to estimate the true calibration error (TCE), is designed. $TCE_{bpm}$ is proven to be a consistent calibration measure. Furthermore, realistic calibration datasets can be generated by the binomial process modeling from a preset true calibration curve and confidence score distribution, which can serve as a benchmark to measure and compare the discrepancy between existing calibration metrics and the true calibration error. The effectiveness of our calibration method and metric are verified in real-world and simulated data.

Canonical Correlation Guided Deep Neural Network

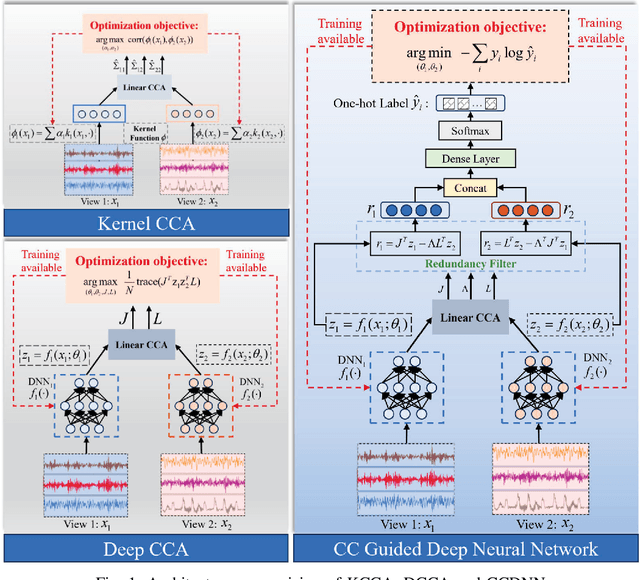
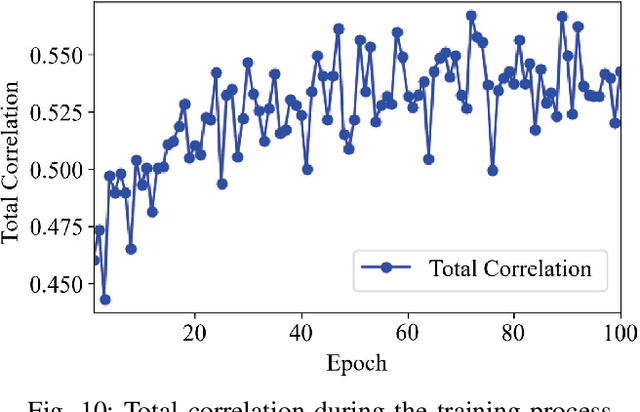
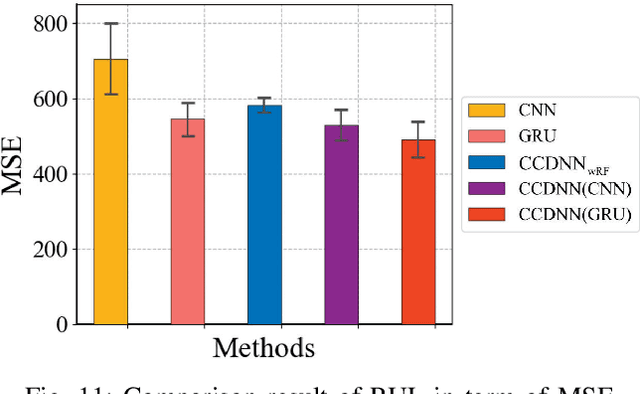
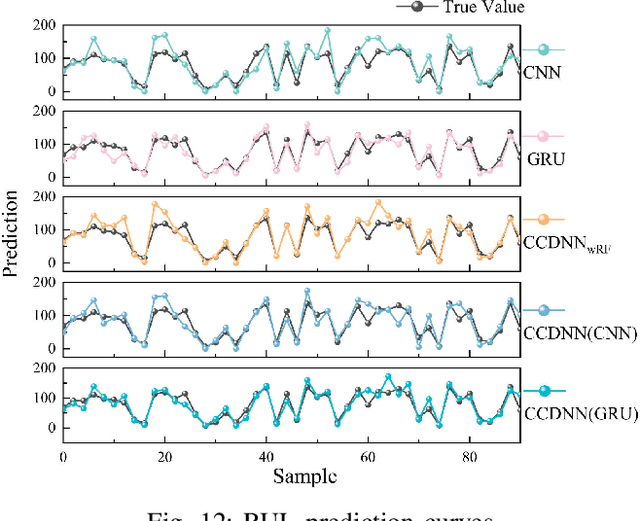
Learning representations of two views of data such that the resulting representations are highly linearly correlated is appealing in machine learning. In this paper, we present a canonical correlation guided learning framework, which allows to be realized by deep neural networks (CCDNN), to learn such a correlated representation. It is also a novel merging of multivariate analysis (MVA) and machine learning, which can be viewed as transforming MVA into end-to-end architectures with the aid of neural networks. Unlike the linear canonical correlation analysis (CCA), kernel CCA and deep CCA, in the proposed method, the optimization formulation is not restricted to maximize correlation, instead we make canonical correlation as a constraint, which preserves the correlated representation learning ability and focuses more on the engineering tasks endowed by optimization formulation, such as reconstruction, classification and prediction. Furthermore, to reduce the redundancy induced by correlation, a redundancy filter is designed. We illustrate the performance of CCDNN on various tasks. In experiments on MNIST dataset, the results show that CCDNN has better reconstruction performance in terms of mean squared error and mean absolute error than DCCA and DCCAE. Also, we present the application of the proposed network to industrial fault diagnosis and remaining useful life cases for the classification and prediction tasks accordingly. The proposed method demonstrates superior performance in both tasks when compared to existing methods. Extension of CCDNN to much more deeper with the aid of residual connection is also presented in appendix.

Neuro-Symbolic Hierarchical Rule Induction

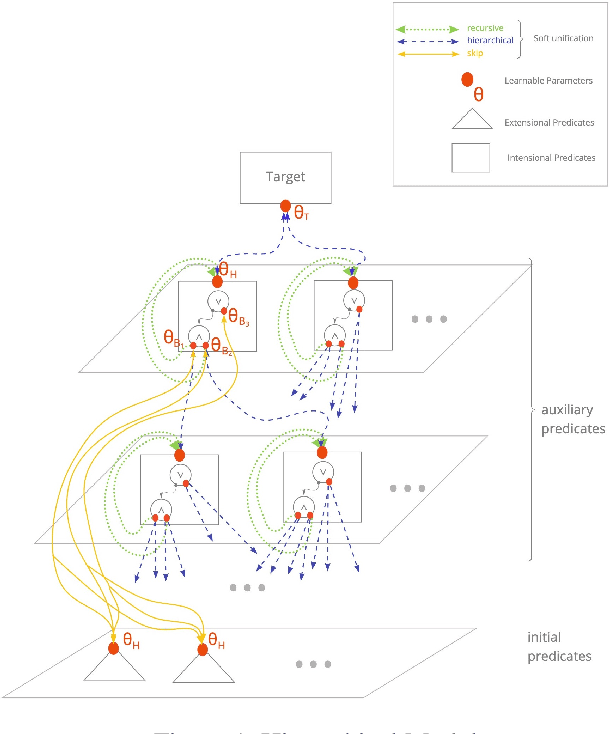
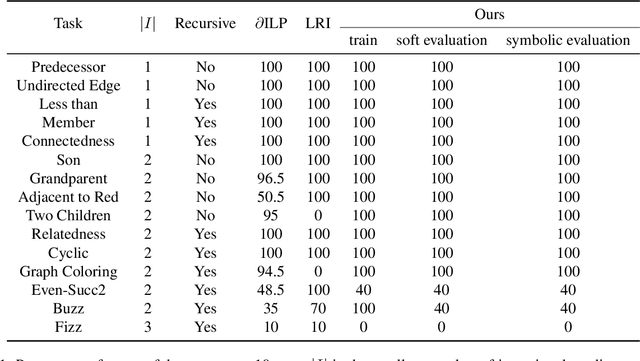
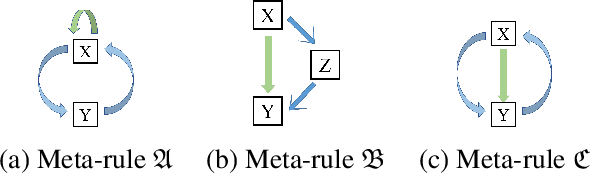
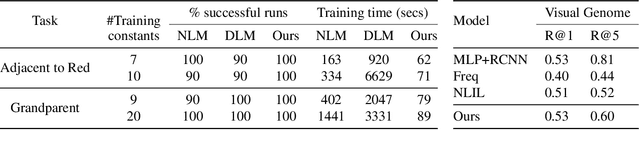
We propose an efficient interpretable neuro-symbolic model to solve Inductive Logic Programming (ILP) problems. In this model, which is built from a set of meta-rules organised in a hierarchical structure, first-order rules are invented by learning embeddings to match facts and body predicates of a meta-rule. To instantiate it, we specifically design an expressive set of generic meta-rules, and demonstrate they generate a consequent fragment of Horn clauses. During training, we inject a controlled \pw{Gumbel} noise to avoid local optima and employ interpretability-regularization term to further guide the convergence to interpretable rules. We empirically validate our model on various tasks (ILP, visual genome, reinforcement learning) against several state-of-the-art methods.

Differentiable Logic Machines

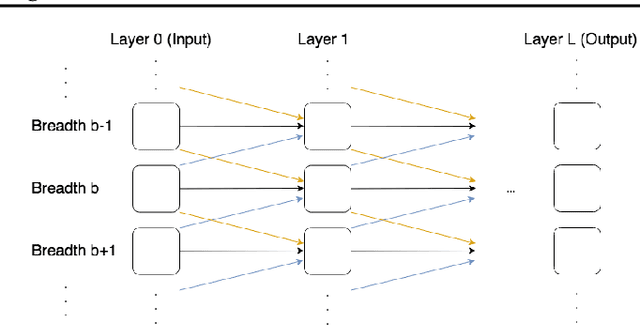
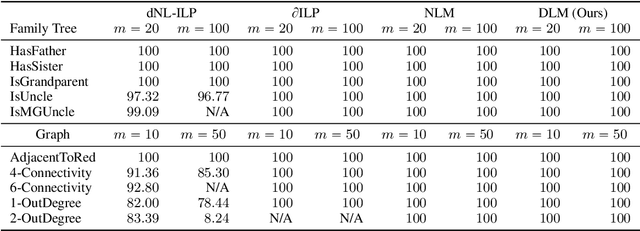
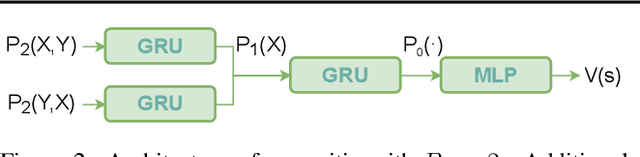
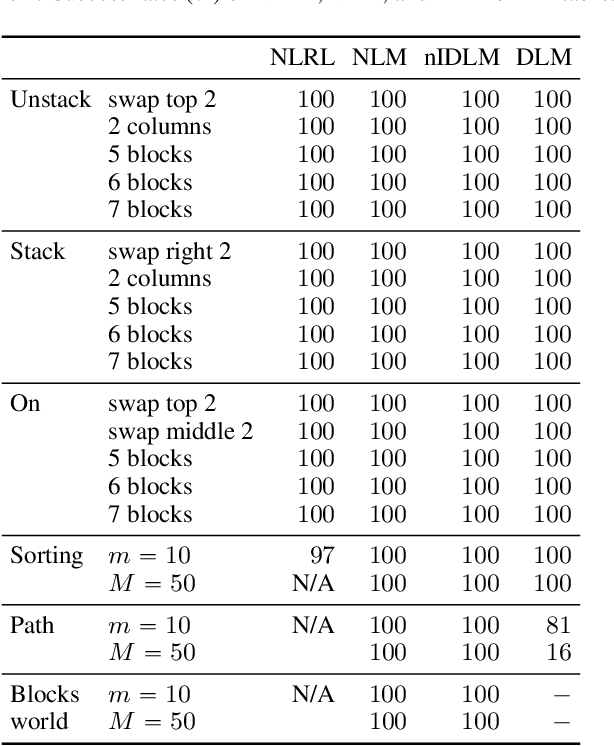
The integration of reasoning, learning, and decision-making is key to build more general AI systems. As a step in this direction, we propose a novel neural-logic architecture that can solve both inductive logic programming (ILP) and deep reinforcement learning (RL) problems. Our architecture defines a restricted but expressive continuous space of first-order logic programs by assigning weights to predicates instead of rules. Therefore, it is fully differentiable and can be efficiently trained with gradient descent. Besides, in the deep RL setting with actor-critic algorithms, we propose a novel efficient critic architecture. Compared to state-of-the-art methods on both ILP and RL problems, our proposition achieves excellent performance, while being able to provide a fully interpretable solution and scaling much better, especially during the testing phase.