Canonical Correlation Guided Deep Neural Network
Paper and Code
Sep 28, 2024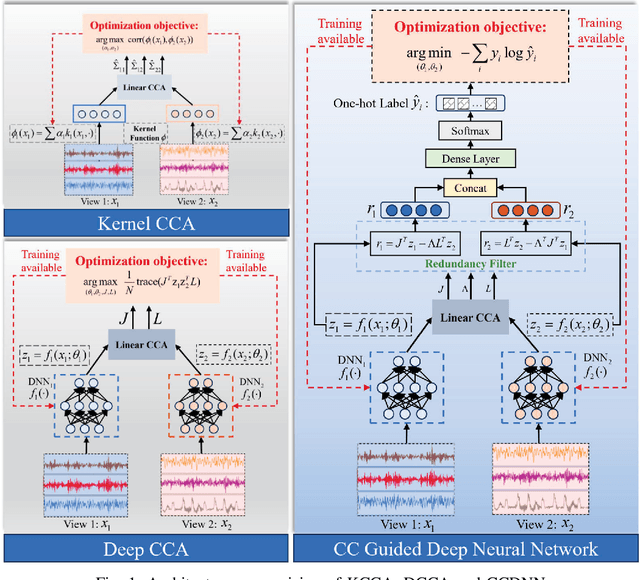
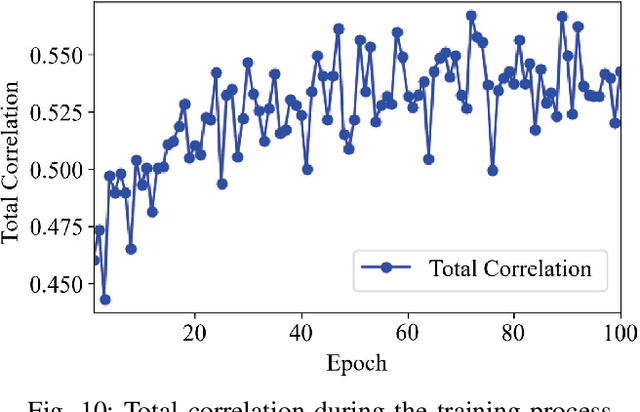
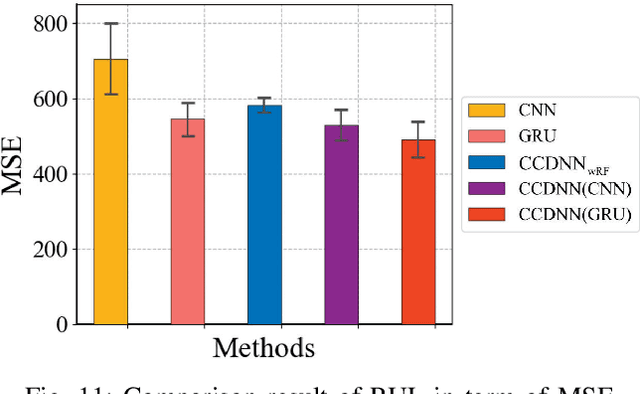
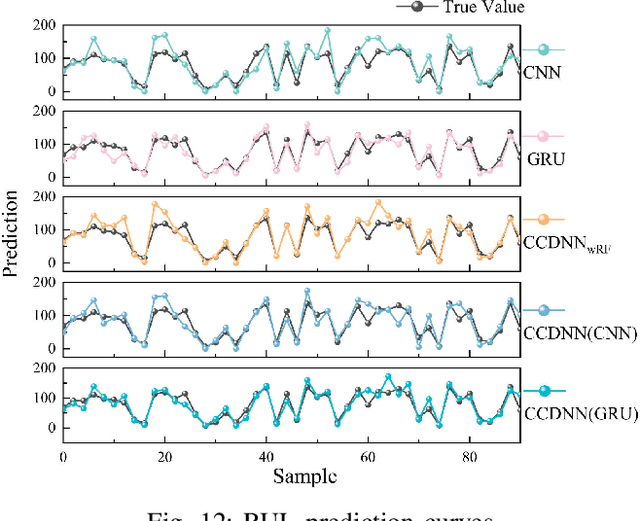
Learning representations of two views of data such that the resulting representations are highly linearly correlated is appealing in machine learning. In this paper, we present a canonical correlation guided learning framework, which allows to be realized by deep neural networks (CCDNN), to learn such a correlated representation. It is also a novel merging of multivariate analysis (MVA) and machine learning, which can be viewed as transforming MVA into end-to-end architectures with the aid of neural networks. Unlike the linear canonical correlation analysis (CCA), kernel CCA and deep CCA, in the proposed method, the optimization formulation is not restricted to maximize correlation, instead we make canonical correlation as a constraint, which preserves the correlated representation learning ability and focuses more on the engineering tasks endowed by optimization formulation, such as reconstruction, classification and prediction. Furthermore, to reduce the redundancy induced by correlation, a redundancy filter is designed. We illustrate the performance of CCDNN on various tasks. In experiments on MNIST dataset, the results show that CCDNN has better reconstruction performance in terms of mean squared error and mean absolute error than DCCA and DCCAE. Also, we present the application of the proposed network to industrial fault diagnosis and remaining useful life cases for the classification and prediction tasks accordingly. The proposed method demonstrates superior performance in both tasks when compared to existing methods. Extension of CCDNN to much more deeper with the aid of residual connection is also presented in appendix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge