Smart Picks in the Dark: Towards Efficient RLVR for Reasoning via Tracing Metacognitive Pivots

Reinforcement learning with verifiable rewards (RLVR) has greatly advanced large reasoning models (LRMs), but it requires timely training on a huge fully-annotated dataset. To this end, data-efficient RLVR methods have been widely studied from two perspectives: (i) data selection methods identify a small subset of "golden" samples that yield near-full-data performance, but they rely on a pre-existing pool of labeled data. (ii) unsupervised RLVR methods train the model using its own internal supervision signals on large-scale unlabeled data, yet they exhibit suboptimal performance. Accordingly, we investigate the "pick in the dark" setup for RLVR, which aims to select, without prior supervision, unlabeled samples that are most beneficial for training and worthy of annotation. Through systematic analysis, we demonstrate that smart picks hinge on a well-calibrated uncertainty estimator to enable strategic partitioning of data for adaptive training regimes. Building on this insight, we propose PivotTrace, a three-way data triage framework that leverages attention dynamics to trace metacognitive pivots during reasoning. By precisely quantifying uncertainty through pivot density, PivotTrace achieves automated data routing to synergistically maximize both annotation and training efficiency. Empirically, PivotTrace surpasses the fully supervised LRM with only 29.3% annotated samples and 2.75 faster convergence.

GeoMin: Data-Efficient Semi-Supervised RLVR via Geometric Distribution Modeling

Reinforcement learning with verifiable rewards (RLVR) significantly advances LLM reasoning, yet it faces a dilemma: standard supervised scaling is throttled by high annotation costs, while unsupervised alternatives suffer from severe model collapse. Recent semi-supervised RLVR methods address this by using a small labeled set to guide unlabeled data, achieving a promising trade-off between training efficacy and annotation cost. However, they suffer from a severe data-efficiency bottleneck due to the reliance on coarse performance heuristics, leaving a vast majority of valuable instances underutilized. To this end, we propose GeoMin, which models global feature distributions on labeled data to decode the structural discrepancy between correct and incorrect rollouts, thereby establishing a robust prior to assess the reliability of self-reward signals and fully unleash the potential of unlabeled data. Empirically, GeoMin outperforms the strongest baselines by +4.1% and even surpasses fully supervised models with only 10% of the annotations, demonstrating remarkable data efficiency.

Neuro-Symbolic Hierarchical Rule Induction

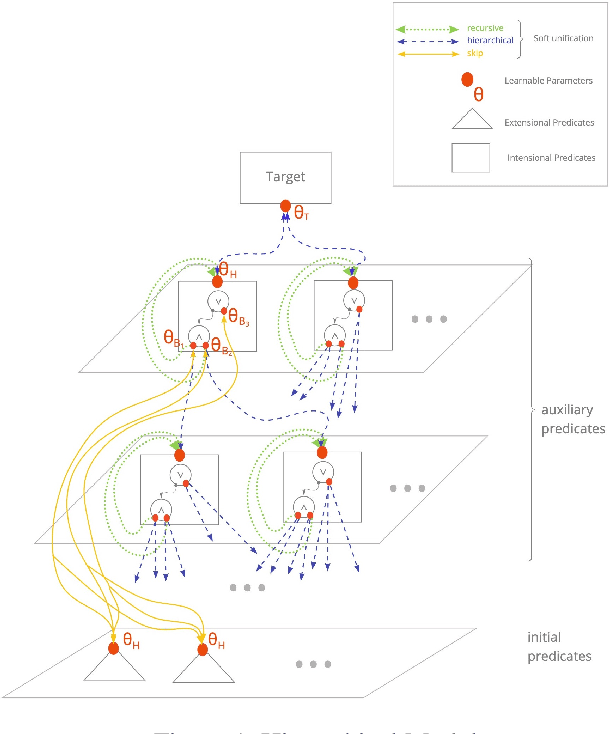
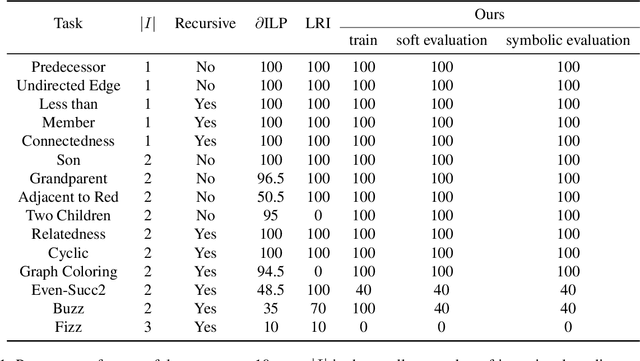
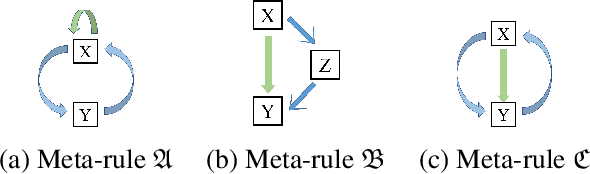
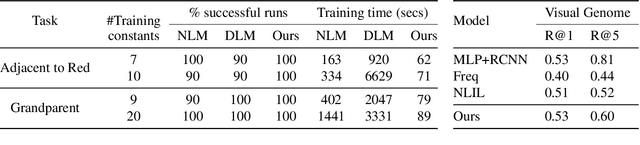
We propose an efficient interpretable neuro-symbolic model to solve Inductive Logic Programming (ILP) problems. In this model, which is built from a set of meta-rules organised in a hierarchical structure, first-order rules are invented by learning embeddings to match facts and body predicates of a meta-rule. To instantiate it, we specifically design an expressive set of generic meta-rules, and demonstrate they generate a consequent fragment of Horn clauses. During training, we inject a controlled \pw{Gumbel} noise to avoid local optima and employ interpretability-regularization term to further guide the convergence to interpretable rules. We empirically validate our model on various tasks (ILP, visual genome, reinforcement learning) against several state-of-the-art methods.

Differentiable Logic Machines

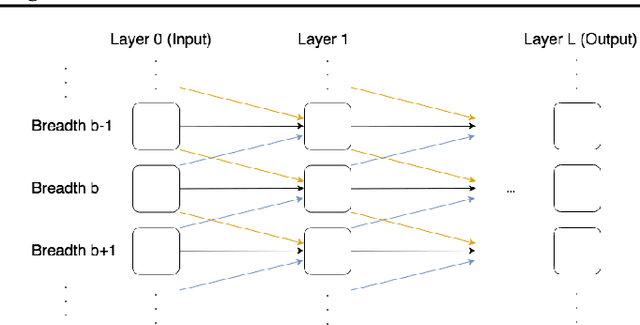
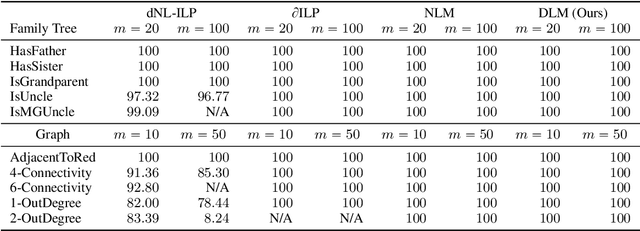
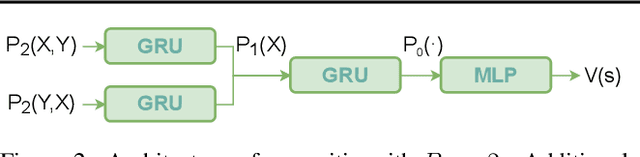
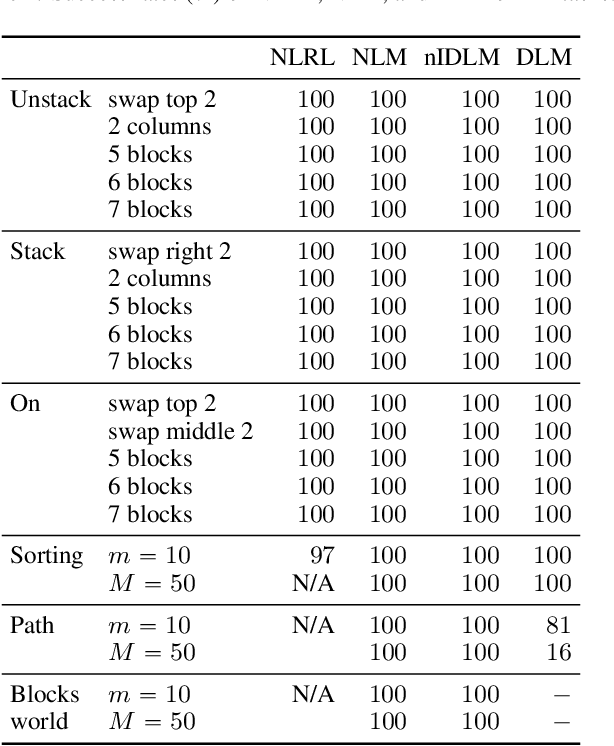
The integration of reasoning, learning, and decision-making is key to build more general AI systems. As a step in this direction, we propose a novel neural-logic architecture that can solve both inductive logic programming (ILP) and deep reinforcement learning (RL) problems. Our architecture defines a restricted but expressive continuous space of first-order logic programs by assigning weights to predicates instead of rules. Therefore, it is fully differentiable and can be efficiently trained with gradient descent. Besides, in the deep RL setting with actor-critic algorithms, we propose a novel efficient critic architecture. Compared to state-of-the-art methods on both ILP and RL problems, our proposition achieves excellent performance, while being able to provide a fully interpretable solution and scaling much better, especially during the testing phase.