Neuro-Symbolic Hierarchical Rule Induction
Paper and Code
Dec 26, 2021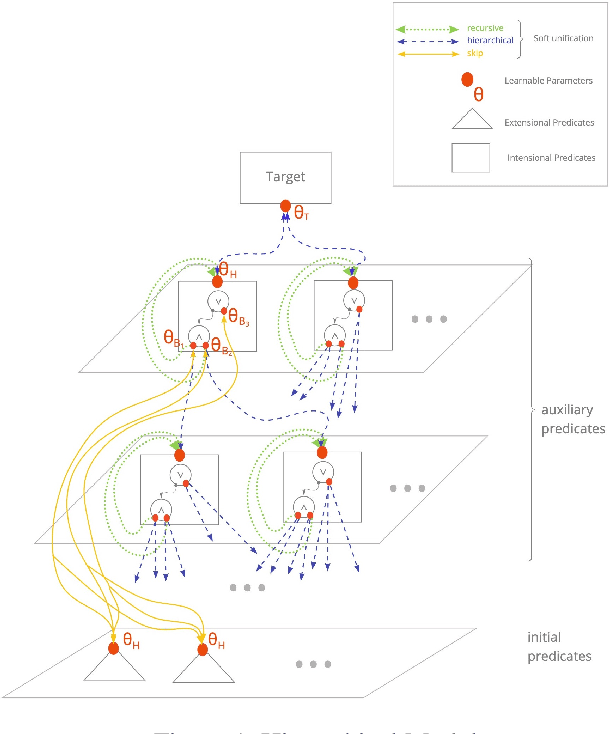
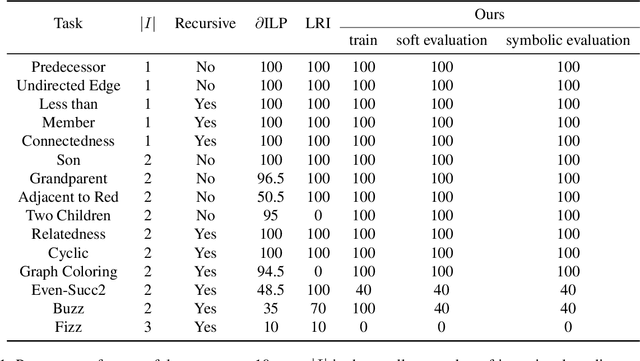
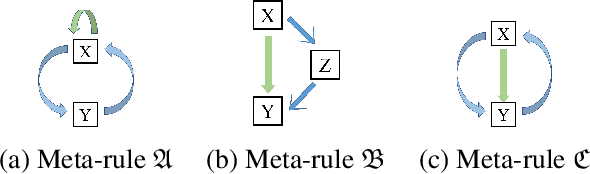
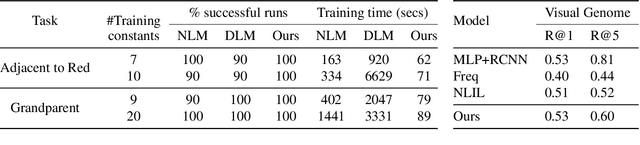
We propose an efficient interpretable neuro-symbolic model to solve Inductive Logic Programming (ILP) problems. In this model, which is built from a set of meta-rules organised in a hierarchical structure, first-order rules are invented by learning embeddings to match facts and body predicates of a meta-rule. To instantiate it, we specifically design an expressive set of generic meta-rules, and demonstrate they generate a consequent fragment of Horn clauses. During training, we inject a controlled \pw{Gumbel} noise to avoid local optima and employ interpretability-regularization term to further guide the convergence to interpretable rules. We empirically validate our model on various tasks (ILP, visual genome, reinforcement learning) against several state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge