Combining Priors with Experience: Confidence Calibration Based on Binomial Process Modeling
Paper and Code
Dec 18, 2024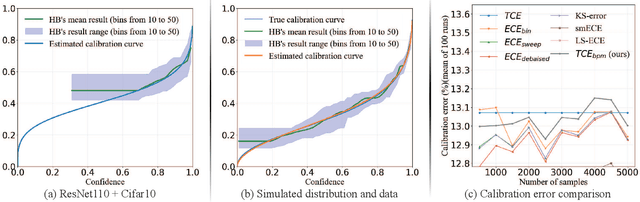
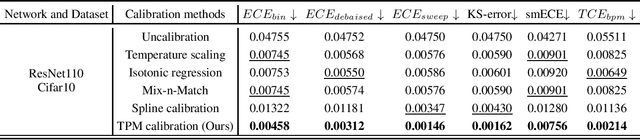

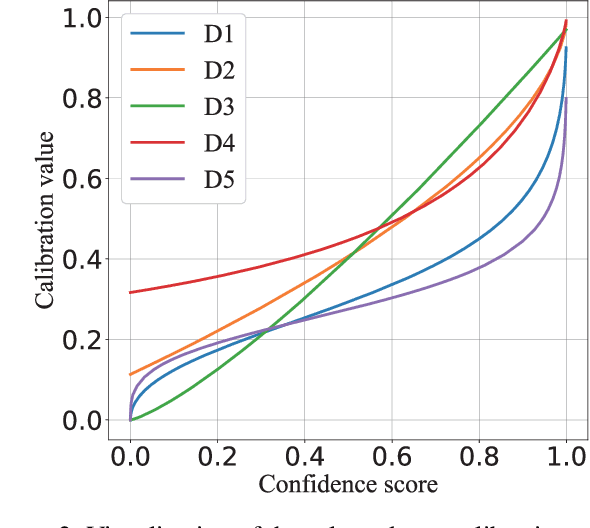
Confidence calibration of classification models is a technique to estimate the true posterior probability of the predicted class, which is critical for ensuring reliable decision-making in practical applications. Existing confidence calibration methods mostly use statistical techniques to estimate the calibration curve from data or fit a user-defined calibration function, but often overlook fully mining and utilizing the prior distribution behind the calibration curve. However, a well-informed prior distribution can provide valuable insights beyond the empirical data under the limited data or low-density regions of confidence scores. To fill this gap, this paper proposes a new method that integrates the prior distribution behind the calibration curve with empirical data to estimate a continuous calibration curve, which is realized by modeling the sampling process of calibration data as a binomial process and maximizing the likelihood function of the binomial process. We prove that the calibration curve estimating method is Lipschitz continuous with respect to data distribution and requires a sample size of $3/B$ of that required for histogram binning, where $B$ represents the number of bins. Also, a new calibration metric ($TCE_{bpm}$), which leverages the estimated calibration curve to estimate the true calibration error (TCE), is designed. $TCE_{bpm}$ is proven to be a consistent calibration measure. Furthermore, realistic calibration datasets can be generated by the binomial process modeling from a preset true calibration curve and confidence score distribution, which can serve as a benchmark to measure and compare the discrepancy between existing calibration metrics and the true calibration error. The effectiveness of our calibration method and metric are verified in real-world and simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge