Anatomical Structure-Guided Medical Vision-Language Pre-training

Learning medical visual representations through vision-language pre-training has reached remarkable progress. Despite the promising performance, it still faces challenges, i.e., local alignment lacks interpretability and clinical relevance, and the insufficient internal and external representation learning of image-report pairs. To address these issues, we propose an Anatomical Structure-Guided (ASG) framework. Specifically, we parse raw reports into triplets <anatomical region, finding, existence>, and fully utilize each element as supervision to enhance representation learning. For anatomical region, we design an automatic anatomical region-sentence alignment paradigm in collaboration with radiologists, considering them as the minimum semantic units to explore fine-grained local alignment. For finding and existence, we regard them as image tags, applying an image-tag recognition decoder to associate image features with their respective tags within each sample and constructing soft labels for contrastive learning to improve the semantic association of different image-report pairs. We evaluate the proposed ASG framework on two downstream tasks, including five public benchmarks. Experimental results demonstrate that our method outperforms the state-of-the-art methods.

An Improved Online Penalty Parameter Selection Procedure for $\ell_1$-Penalized Autoregressive with Exogenous Variables

Many recent developments in the high-dimensional statistical time series literature have centered around time-dependent applications that can be adapted to regularized least squares. Of particular interest is the lasso, which both serves to regularize and provide feature selection. The lasso requires the specification of a penalty parameter that determines the degree of sparsity to impose. The most popular penalty parameter selection approaches that respect time dependence are very computationally intensive and are not appropriate for modeling certain classes of time series. We propose enhancing a canonical time series model, the autoregressive model with exogenous variables, with a novel online penalty parameter selection procedure that takes advantage of the sequential nature of time series data to improve both computational performance and forecast accuracy relative to existing methods in both a simulation and empirical application involving macroeconomic indicators.

On a Bernoulli Autoregression Framework for Link Discovery and Prediction

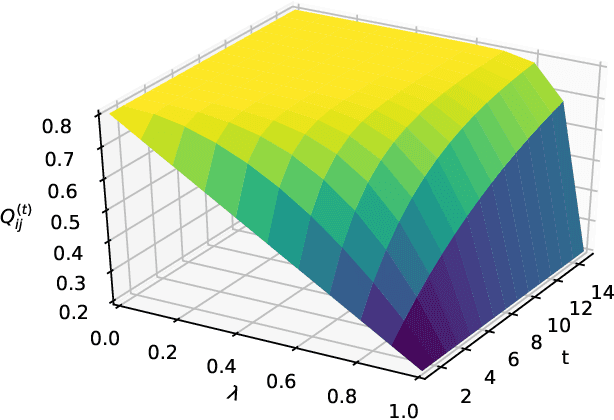
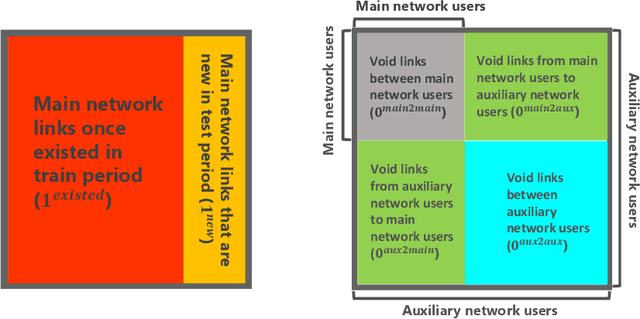
We present a dynamic prediction framework for binary sequences that is based on a Bernoulli generalization of the auto-regressive process. Our approach lends itself easily to variants of the standard link prediction problem for a sequence of time dependent networks. Focusing on this dynamic network link prediction/recommendation task, we propose a novel problem that exploits additional information via a much larger sequence of auxiliary networks and has important real-world relevance. To allow discovery of links that do not exist in the available data, our model estimation framework introduces a regularization term that presents a trade-off between the conventional link prediction and this discovery task. In contrast to existing work our stochastic gradient based estimation approach is highly efficient and can scale to networks with millions of nodes. We show extensive empirical results on both actual product-usage based time dependent networks and also present results on a Reddit based data set of time dependent sentiment sequences.

Testing for Conditional Mean Independence with Covariates through Martingale Difference Divergence

As a crucial problem in statistics is to decide whether additional variables are needed in a regression model. We propose a new multivariate test to investigate the conditional mean independence of Y given X conditioning on some known effect Z, i.e., E(Y|X, Z) = E(Y|Z). Assuming that E(Y|Z) and Z are linearly related, we reformulate an equivalent notion of conditional mean independence through transformation, which is approximated in practice. We apply the martingale difference divergence (Shao and Zhang, 2014) to measure conditional mean dependence, and show that the estimation error from approximation is negligible, as it has no impact on the asymptotic distribution of the test statistic under some regularity assumptions. The implementation of our test is demonstrated by both simulations and a financial data example.

Rare Feature Selection in High Dimensions

It is common in modern prediction problems for many predictor variables to be counts of rarely occurring events. This leads to design matrices in which many columns are highly sparse. The challenge posed by such "rare features" has received little attention despite its prevalence in diverse areas, ranging from natural language processing (e.g., rare words) to biology (e.g., rare species). We show, both theoretically and empirically, that not explicitly accounting for the rareness of features can greatly reduce the effectiveness of an analysis. We next propose a framework for aggregating rare features into denser features in a flexible manner that creates better predictors of the response. Our strategy leverages side information in the form of a tree that encodes feature similarity. We apply our method to data from TripAdvisor, in which we predict the numerical rating of a hotel based on the text of the associated review. Our method achieves high accuracy by making effective use of rare words; by contrast, the lasso is unable to identify highly predictive words if they are too rare. A companion R package, called rare, implements our new estimator, using the alternating direction method of multipliers.

Hierarchical Sparse Modeling: A Choice of Two Group Lasso Formulations

Demanding sparsity in estimated models has become a routine practice in statistics. In many situations, we wish to require that the sparsity patterns attained honor certain problem-specific constraints. Hierarchical sparse modeling (HSM) refers to situations in which these constraints specify that one set of parameters be set to zero whenever another is set to zero. In recent years, numerous papers have developed convex regularizers for this form of sparsity structure, which arises in many areas of statistics including interaction modeling, time series analysis, and covariance estimation. In this paper, we observe that these methods fall into two frameworks, the group lasso (GL) and latent overlapping group lasso (LOG), which have not been systematically compared in the context of HSM. The purpose of this paper is to provide a side-by-side comparison of these two frameworks for HSM in terms of their statistical properties and computational efficiency. We call special attention to GL's more aggressive shrinkage of parameters deep in the hierarchy, a property not shared by LOG. In terms of computation, we introduce a finite-step algorithm that exactly solves the proximal operator of LOG for a certain simple HSM structure; we later exploit this to develop a novel path-based block coordinate descent scheme for general HSM structures. Both algorithms greatly improve the computational performance of LOG. Finally, we compare the two methods in the context of covariance estimation, where we introduce a new sparsely-banded estimator using LOG, which we show achieves the statistical advantages of an existing GL-based method but is simpler to express and more efficient to compute.