On a Bernoulli Autoregression Framework for Link Discovery and Prediction

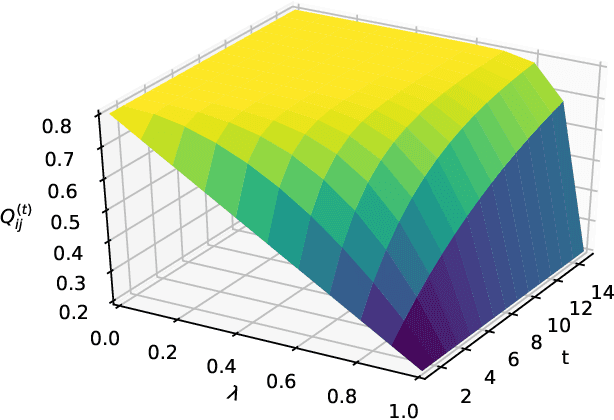
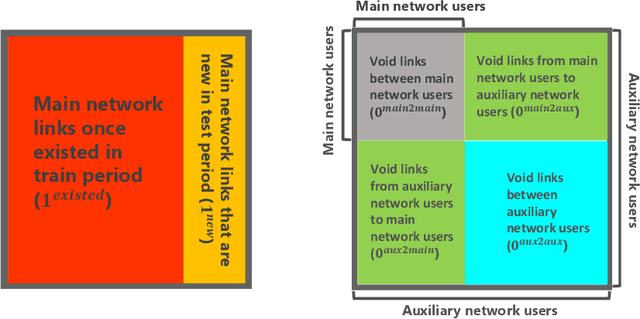
We present a dynamic prediction framework for binary sequences that is based on a Bernoulli generalization of the auto-regressive process. Our approach lends itself easily to variants of the standard link prediction problem for a sequence of time dependent networks. Focusing on this dynamic network link prediction/recommendation task, we propose a novel problem that exploits additional information via a much larger sequence of auxiliary networks and has important real-world relevance. To allow discovery of links that do not exist in the available data, our model estimation framework introduces a regularization term that presents a trade-off between the conventional link prediction and this discovery task. In contrast to existing work our stochastic gradient based estimation approach is highly efficient and can scale to networks with millions of nodes. We show extensive empirical results on both actual product-usage based time dependent networks and also present results on a Reddit based data set of time dependent sentiment sequences.

On Selecting Stable Predictors in Time Series Models

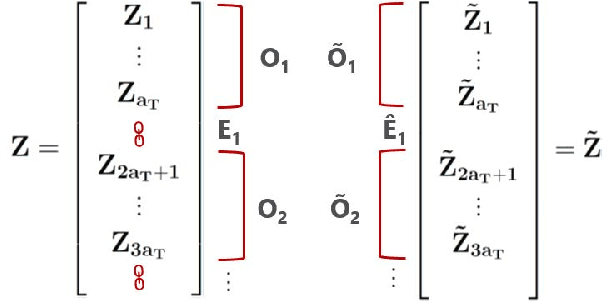
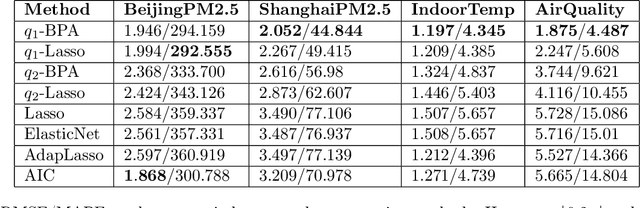
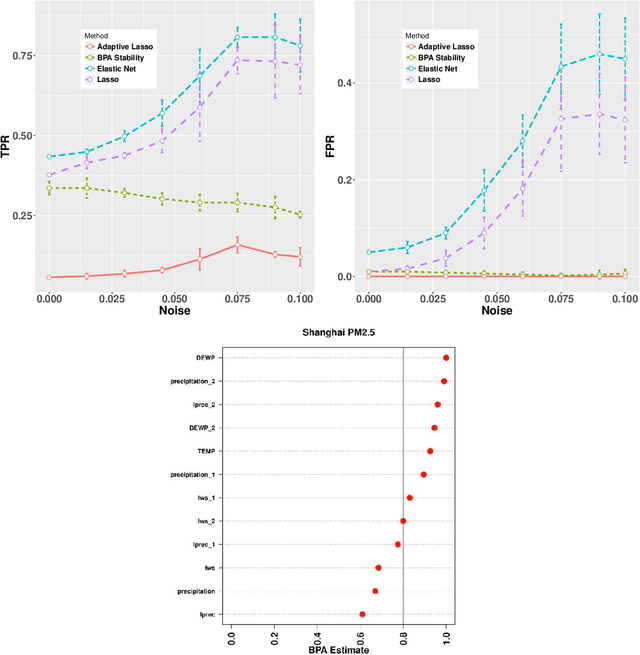
We extend the feature selection methodology to dependent data and propose a novel time series predictor selection scheme that accommodates statistical dependence in a more typical i.i.d sub-sampling based framework. Furthermore, the machinery of mixing stationary processes allows us to quantify the improvements of our approach over any base predictor selection method (such as lasso) even in a finite sample setting. Using the lasso as a base procedure we demonstrate the applicability of our methods to simulated and several real time series datasets.

Data Dependent Convergence for Distributed Stochastic Optimization

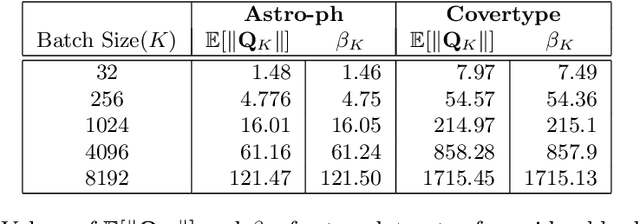
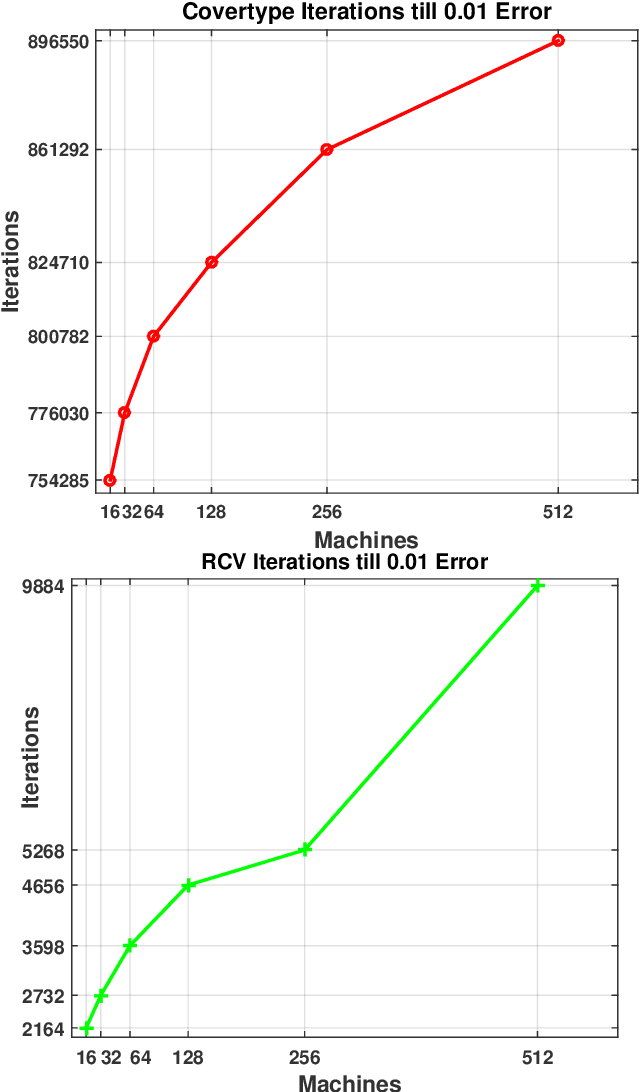
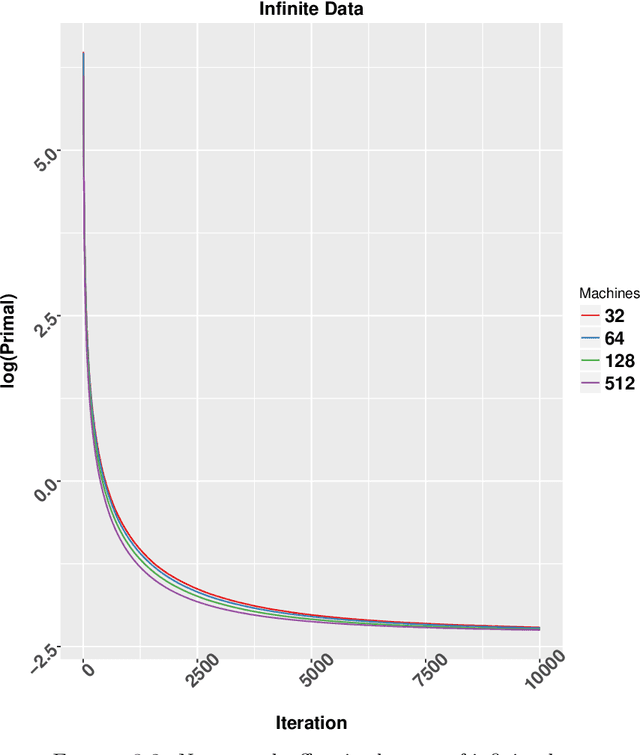
In this dissertation we propose alternative analysis of distributed stochastic gradient descent (SGD) algorithms that rely on spectral properties of the data covariance. As a consequence we can relate questions pertaining to speedups and convergence rates for distributed SGD to the data distribution instead of the regularity properties of the objective functions. More precisely we show that this rate depends on the spectral norm of the sample covariance matrix. An estimate of this norm can provide practitioners with guidance towards a potential gain in algorithm performance. For example many sparse datasets with low spectral norm prove to be amenable to gains in distributed settings. Towards establishing this data dependence we first study a distributed consensus-based SGD algorithm and show that the rate of convergence involves the spectral norm of the sample covariance matrix when the underlying data is assumed to be independent and identically distributed (homogenous). This dependence allows us to identify network regimes that prove to be beneficial for datasets with low sample covariance spectral norm. Existing consensus based analyses prove to be sub-optimal in the homogenous setting. Our analysis method also allows us to find data-dependent convergence rates as we limit the amount of communication. Spreading a fixed amount of data across more nodes slows convergence; in the asymptotic regime we show that adding more machines can help when minimizing twice-differentiable losses. Since the mini-batch results don't follow from the consensus results we propose a different data dependent analysis thereby providing theoretical validation for why certain datasets are more amenable to mini-batching. We also provide empirical evidence for results in this thesis.

Semi-supervised Learning with Density Based Distances

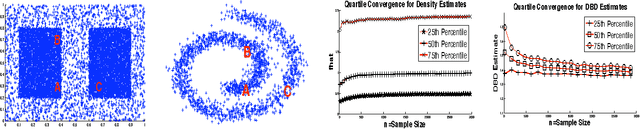
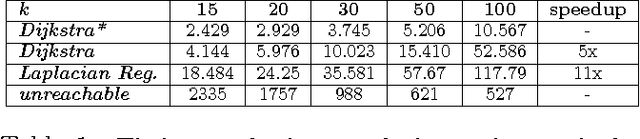
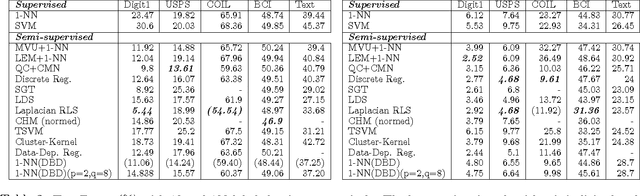
We present a simple, yet effective, approach to Semi-Supervised Learning. Our approach is based on estimating density-based distances (DBD) using a shortest path calculation on a graph. These Graph-DBD estimates can then be used in any distance-based supervised learning method, such as Nearest Neighbor methods and SVMs with RBF kernels. In order to apply the method to very large data sets, we also present a novel algorithm which integrates nearest neighbor computations into the shortest path search and can find exact shortest paths even in extremely large dense graphs. Significant runtime improvement over the commonly used Laplacian regularization method is then shown on a large scale dataset.