Data Dependent Convergence for Distributed Stochastic Optimization
Paper and Code
Aug 30, 2016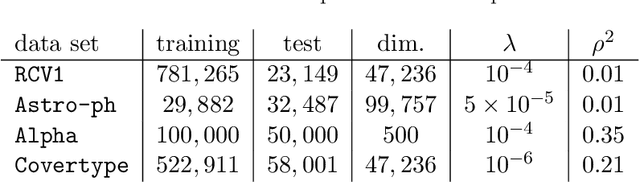
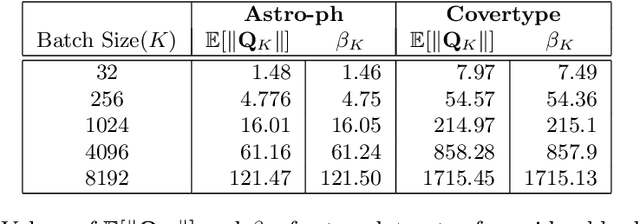
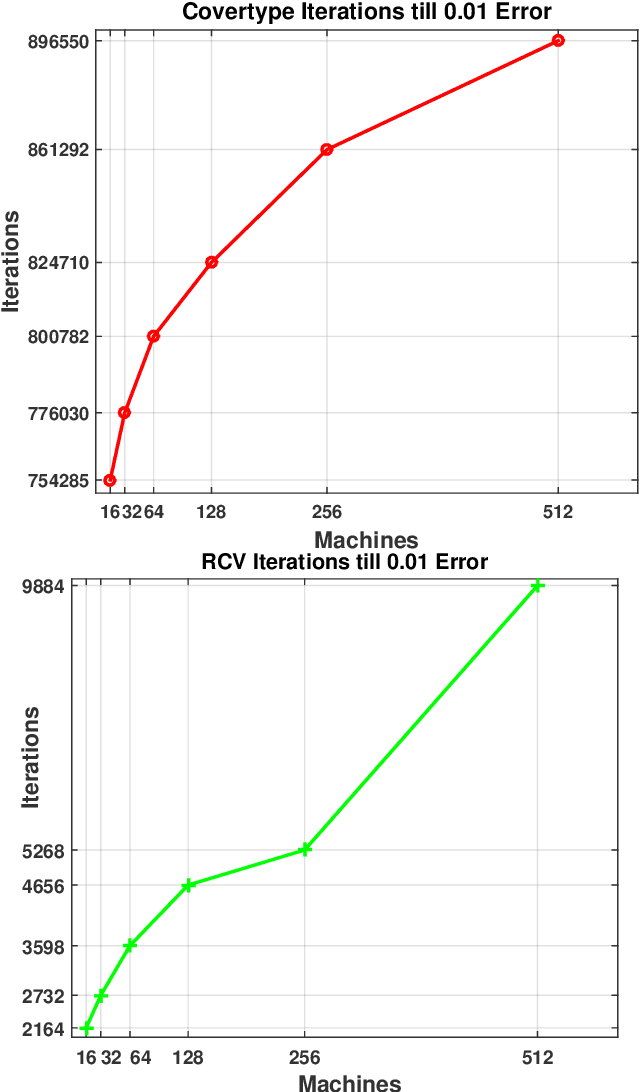
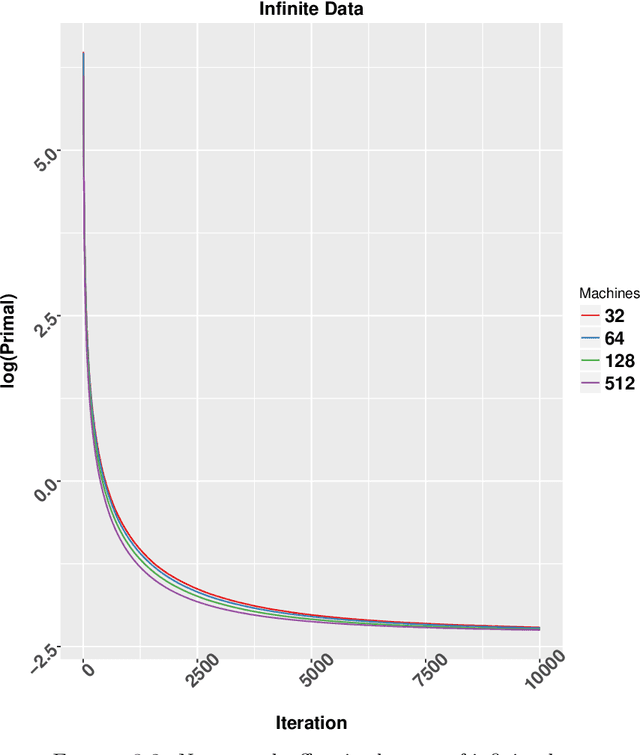
In this dissertation we propose alternative analysis of distributed stochastic gradient descent (SGD) algorithms that rely on spectral properties of the data covariance. As a consequence we can relate questions pertaining to speedups and convergence rates for distributed SGD to the data distribution instead of the regularity properties of the objective functions. More precisely we show that this rate depends on the spectral norm of the sample covariance matrix. An estimate of this norm can provide practitioners with guidance towards a potential gain in algorithm performance. For example many sparse datasets with low spectral norm prove to be amenable to gains in distributed settings. Towards establishing this data dependence we first study a distributed consensus-based SGD algorithm and show that the rate of convergence involves the spectral norm of the sample covariance matrix when the underlying data is assumed to be independent and identically distributed (homogenous). This dependence allows us to identify network regimes that prove to be beneficial for datasets with low sample covariance spectral norm. Existing consensus based analyses prove to be sub-optimal in the homogenous setting. Our analysis method also allows us to find data-dependent convergence rates as we limit the amount of communication. Spreading a fixed amount of data across more nodes slows convergence; in the asymptotic regime we show that adding more machines can help when minimizing twice-differentiable losses. Since the mini-batch results don't follow from the consensus results we propose a different data dependent analysis thereby providing theoretical validation for why certain datasets are more amenable to mini-batching. We also provide empirical evidence for results in this thesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge