Generating coherent comic with rich story using ChatGPT and Stable Diffusion

Past work demonstrated that using neural networks, we can extend unfinished music pieces while maintaining the music style of the musician. With recent advancements in large language models and diffusion models, we are now capable of generating comics with an interesting storyline while maintaining the art style of the artist. In this paper, we used ChatGPT to generate storylines and dialogue and then generated the comic using stable diffusion. We introduced a novel way to evaluate AI-generated stories, and we achieved SOTA performance on character fidelity and art style by fine-tuning stable diffusion using LoRA, ControlNet, etc.

Testing for Conditional Mean Independence with Covariates through Martingale Difference Divergence

As a crucial problem in statistics is to decide whether additional variables are needed in a regression model. We propose a new multivariate test to investigate the conditional mean independence of Y given X conditioning on some known effect Z, i.e., E(Y|X, Z) = E(Y|Z). Assuming that E(Y|Z) and Z are linearly related, we reformulate an equivalent notion of conditional mean independence through transformation, which is approximated in practice. We apply the martingale difference divergence (Shao and Zhang, 2014) to measure conditional mean dependence, and show that the estimation error from approximation is negligible, as it has no impact on the asymptotic distribution of the test statistic under some regularity assumptions. The implementation of our test is demonstrated by both simulations and a financial data example.

Independent Component Analysis via Energy-based and Kernel-based Mutual Dependence Measures

We apply both distance-based (Jin and Matteson, 2017) and kernel-based (Pfister et al., 2016) mutual dependence measures to independent component analysis (ICA), and generalize dCovICA (Matteson and Tsay, 2017) to MDMICA, minimizing empirical dependence measures as an objective function in both deflation and parallel manners. Solving this minimization problem, we introduce Latin hypercube sampling (LHS) (McKay et al., 2000), and a global optimization method, Bayesian optimization (BO) (Mockus, 1994) to improve the initialization of the Newton-type local optimization method. The performance of MDMICA is evaluated in various simulation studies and an image data example. When the ICA model is correct, MDMICA achieves competitive results compared to existing approaches. When the ICA model is misspecified, the estimated independent components are less mutually dependent than the observed components using MDMICA, while they are prone to be even more mutually dependent than the observed components using other approaches.

Generalizing Distance Covariance to Measure and Test Multivariate Mutual Dependence

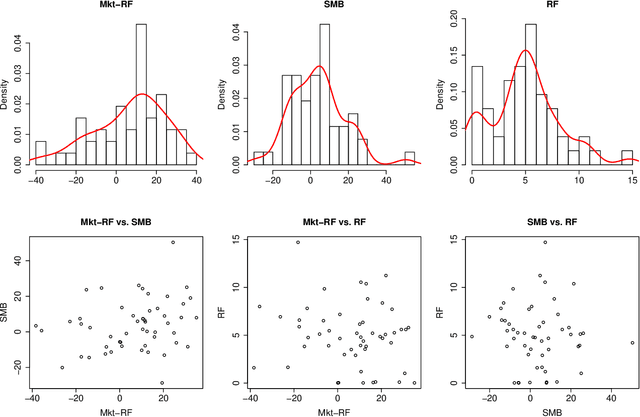
We propose three measures of mutual dependence between multiple random vectors. All the measures are zero if and only if the random vectors are mutually independent. The first measure generalizes distance covariance from pairwise dependence to mutual dependence, while the other two measures are sums of squared distance covariance. All the measures share similar properties and asymptotic distributions to distance covariance, and capture non-linear and non-monotone mutual dependence between the random vectors. Inspired by complete and incomplete V-statistics, we define the empirical measures and simplified empirical measures as a trade-off between the complexity and power when testing mutual independence. Implementation of the tests is demonstrated by both simulation results and real data examples.

Optimization and Testing in Linear Non-Gaussian Component Analysis

Independent component analysis (ICA) decomposes multivariate data into mutually independent components (ICs). The ICA model is subject to a constraint that at most one of these components is Gaussian, which is required for model identifiability. Linear non-Gaussian component analysis (LNGCA) generalizes the ICA model to a linear latent factor model with any number of both non-Gaussian components (signals) and Gaussian components (noise), where observations are linear combinations of independent components. Although the individual Gaussian components are not identifiable, the Gaussian subspace is identifiable. We introduce an estimator along with its optimization approach in which non-Gaussian and Gaussian components are estimated simultaneously, maximizing the discrepancy of each non-Gaussian component from Gaussianity while minimizing the discrepancy of each Gaussian component from Gaussianity. When the number of non-Gaussian components is unknown, we develop a statistical test to determine it based on resampling and the discrepancy of estimated components. Through a variety of simulation studies, we demonstrate the improvements of our estimator over competing estimators, and we illustrate the effectiveness of the test to determine the number of non-Gaussian components. Further, we apply our method to real data examples and demonstrate its practical value.