An Improved Online Penalty Parameter Selection Procedure for $\ell_1$-Penalized Autoregressive with Exogenous Variables

Many recent developments in the high-dimensional statistical time series literature have centered around time-dependent applications that can be adapted to regularized least squares. Of particular interest is the lasso, which both serves to regularize and provide feature selection. The lasso requires the specification of a penalty parameter that determines the degree of sparsity to impose. The most popular penalty parameter selection approaches that respect time dependence are very computationally intensive and are not appropriate for modeling certain classes of time series. We propose enhancing a canonical time series model, the autoregressive model with exogenous variables, with a novel online penalty parameter selection procedure that takes advantage of the sequential nature of time series data to improve both computational performance and forecast accuracy relative to existing methods in both a simulation and empirical application involving macroeconomic indicators.

High Dimensional Forecasting via Interpretable Vector Autoregression

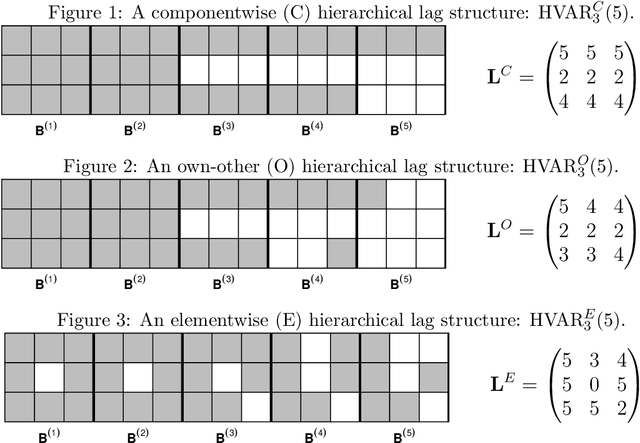
Vector autoregression (VAR) is a fundamental tool for modeling multivariate time series. However, as the number of component series is increased, the VAR model becomes overparameterized. Several authors have addressed this issue by incorporating regularized approaches, such as the lasso in VAR estimation. Traditional approaches address overparameterization by selecting a low lag order, based on the assumption of short range dependence, assuming that a universal lag order applies to all components. Such an approach constrains the relationship between the components and impedes forecast performance. The lasso-based approaches work much better in high-dimensional situations but do not incorporate the notion of lag order selection. We propose a new class of hierarchical lag structures (HLag) that embed the notion of lag selection into a convex regularizer. The key modeling tool is a group lasso with nested groups which guarantees that the sparsity pattern of lag coefficients honors the VAR's ordered structure. The HLag framework offers three structures, which allow for varying levels of flexibility. A simulation study demonstrates improved performance in forecasting and lag order selection over previous approaches, and a macroeconomic application further highlights forecasting improvements as well as HLag's convenient, interpretable output.