Xiang Yang
3rd Workshop on Maritime Computer Vision (MaCVi) 2025: Challenge Results
Jan 17, 2025Abstract:The 3rd Workshop on Maritime Computer Vision (MaCVi) 2025 addresses maritime computer vision for Unmanned Surface Vehicles (USV) and underwater. This report offers a comprehensive overview of the findings from the challenges. We provide both statistical and qualitative analyses, evaluating trends from over 700 submissions. All datasets, evaluation code, and the leaderboard are available to the public at https://macvi.org/workshop/macvi25.
Adaptive DNN Surgery for Selfish Inference Acceleration with On-demand Edge Resource
Jun 21, 2023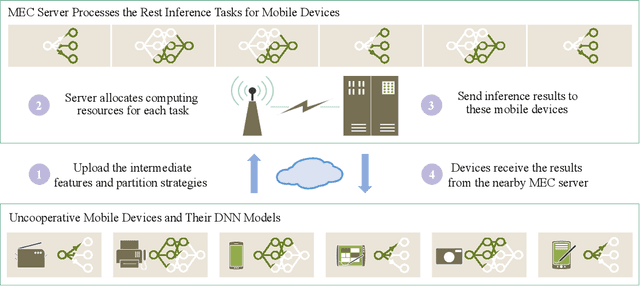
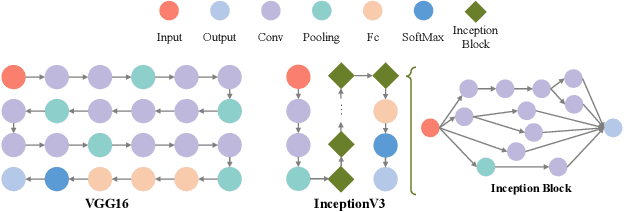
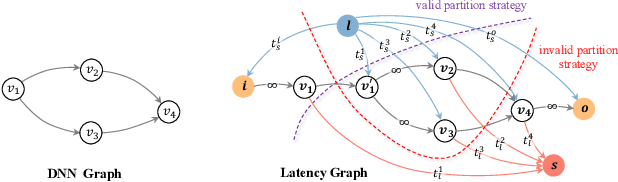
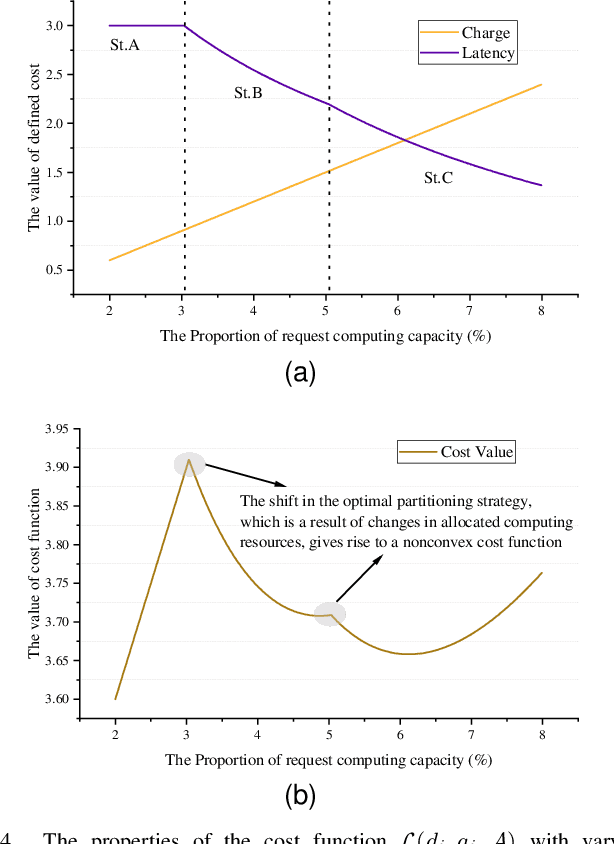
Abstract:Deep Neural Networks (DNNs) have significantly improved the accuracy of intelligent applications on mobile devices. DNN surgery, which partitions DNN processing between mobile devices and multi-access edge computing (MEC) servers, can enable real-time inference despite the computational limitations of mobile devices. However, DNN surgery faces a critical challenge: determining the optimal computing resource demand from the server and the corresponding partition strategy, while considering both inference latency and MEC server usage costs. This problem is compounded by two factors: (1) the finite computing capacity of the MEC server, which is shared among multiple devices, leading to inter-dependent demands, and (2) the shift in modern DNN architecture from chains to directed acyclic graphs (DAGs), which complicates potential solutions. In this paper, we introduce a novel Decentralized DNN Surgery (DDS) framework. We formulate the partition strategy as a min-cut and propose a resource allocation game to adaptively schedule the demands of mobile devices in an MEC environment. We prove the existence of a Nash Equilibrium (NE), and develop an iterative algorithm to efficiently reach the NE for each device. Our extensive experiments demonstrate that DDS can effectively handle varying MEC scenarios, achieving up to 1.25$\times$ acceleration compared to the state-of-the-art algorithm.
Variantional autoencoder with decremental information bottleneck for disentanglement
Mar 22, 2023Abstract:One major challenge of disentanglement learning with variational autoencoders is the trade-off between disentanglement and reconstruction fidelity. Previous incremental methods with only on latent space cannot optimize these two targets simultaneously, so they expand the Information Bottleneck while training to {optimize from disentanglement to reconstruction. However, a large bottleneck will lose the constraint of disentanglement, causing the information diffusion problem. To tackle this issue, we present a novel decremental variational autoencoder with disentanglement-invariant transformations to optimize multiple objectives in different layers, termed DeVAE, for balancing disentanglement and reconstruction fidelity by decreasing the information bottleneck of diverse latent spaces gradually. Benefiting from the multiple latent spaces, DeVAE allows simultaneous optimization of multiple objectives to optimize reconstruction while keeping the constraint of disentanglement, avoiding information diffusion. DeVAE is also compatible with large models with high-dimension latent space. Experimental results on dSprites and Shapes3D that DeVAE achieves \fix{R2q6}{a good balance between disentanglement and reconstruction.DeVAE shows high tolerant of hyperparameters and on high-dimensional latent spaces.
Scale Adaptive Clustering of Multiple Structures
Sep 26, 2017
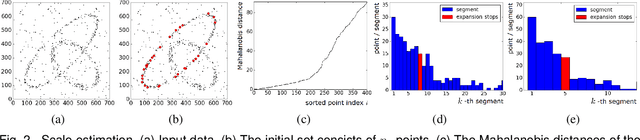

Abstract:We propose the segmentation of noisy datasets into Multiple Inlier Structures with a new Robust Estimator (MISRE). The scale of each individual structure is estimated adaptively from the input data and refined by mean shift, without tuning any parameter in the process, or manually specifying thresholds for different estimation problems. Once all the data points were classified into separate structures, these structures are sorted by their densities with the strongest inlier structures coming out first. Several 2D and 3D synthetic and real examples are presented to illustrate the efficiency, robustness and the limitations of the MISRE algorithm.
Robust Estimation of Multiple Inlier Structures
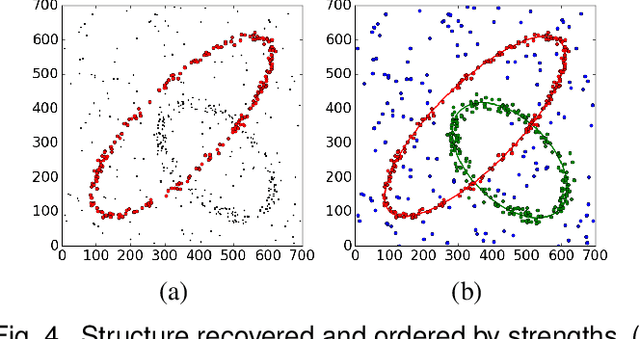
Apr 19, 2017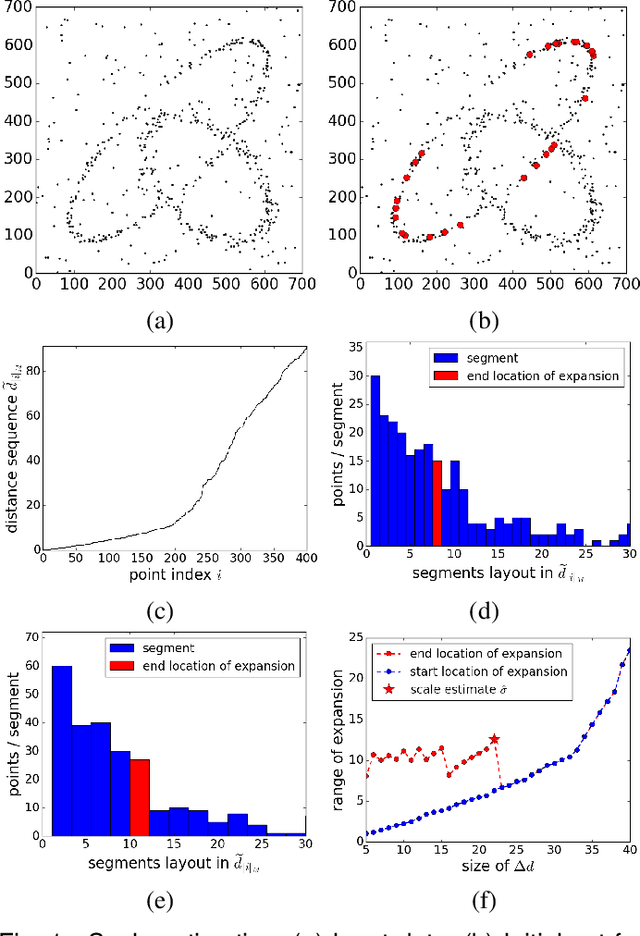

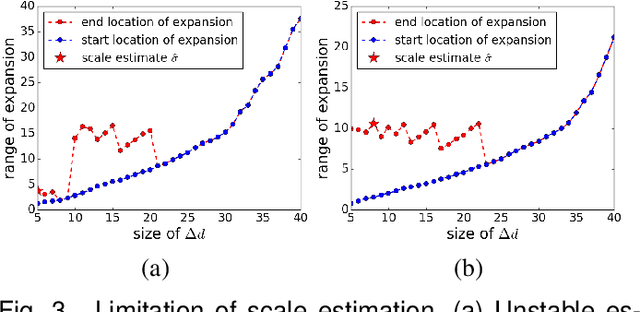
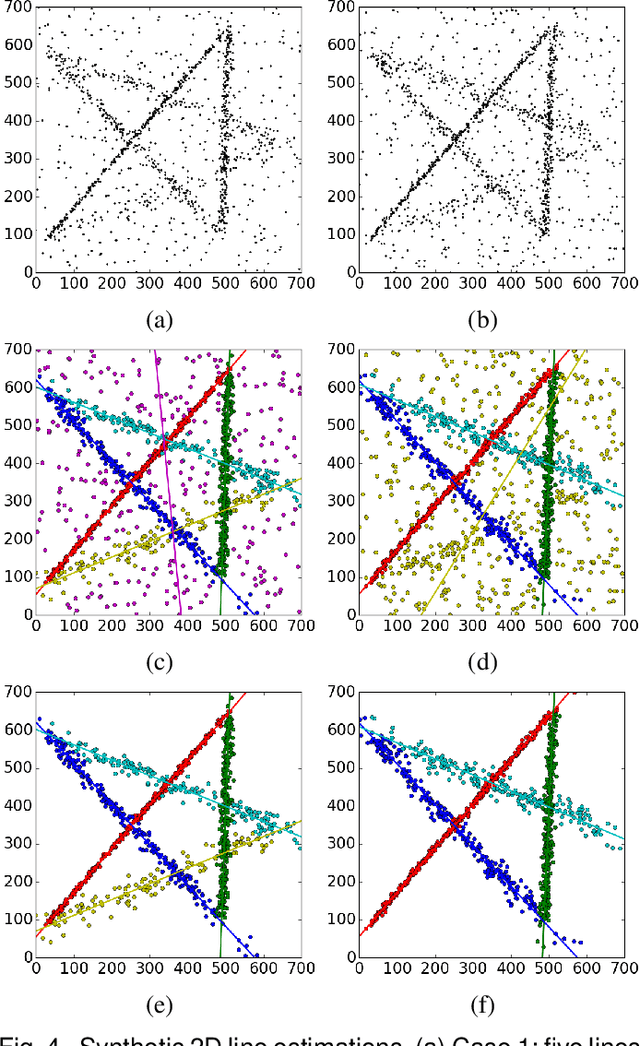
Abstract:The robust estimator presented in this paper processes each structure independently. The scales of the structures are estimated adaptively and no threshold is involved in spite of different objective functions. The user has to specify only the number of elemental subsets for random sampling. After classifying all the input data, the segmented structures are sorted by their strengths and the strongest inlier structures come out at the top. Like any robust estimators, this algorithm also has limitations which are described in detail. Several synthetic and real examples are presented to illustrate every aspect of the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge