Analyzing an Imitation Learning Network for Fundus Image Registration Using a Divide-and-Conquer Approach

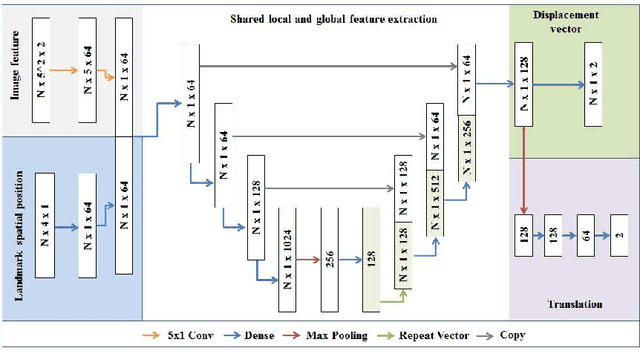
Comparison of microvascular circulation on fundoscopic images is a non-invasive clinical indication for the diagnosis and monitoring of diseases, such as diabetes and hypertensions. The differences between intra-patient images can be assessed quantitatively by registering serial acquisitions. Due to the variability of the images (i.e. contrast, luminosity) and the anatomical changes of the retina, the registration of fundus images remains a challenging task. Recently, several deep learning approaches have been proposed to register fundus images in an end-to-end fashion, achieving remarkable results. However, the results are difficult to interpret and analyze. In this work, we propose an imitation learning framework for the registration of 2D color funduscopic images for a wide range of applications such as disease monitoring, image stitching and super-resolution. We follow a divide-and-conquer approach to improve the interpretability of the proposed network, and analyze both the influence of the input image and the hyperparameters on the registration result. The results show that the proposed registration network reduces the initial target registration error up to 95\%.

What Do We Really Need? Degenerating U-Net on Retinal Vessel Segmentation

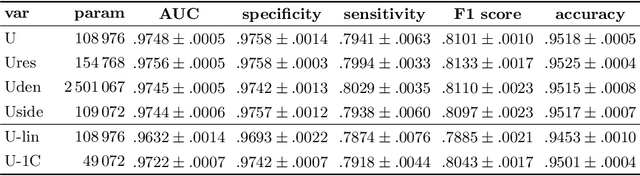
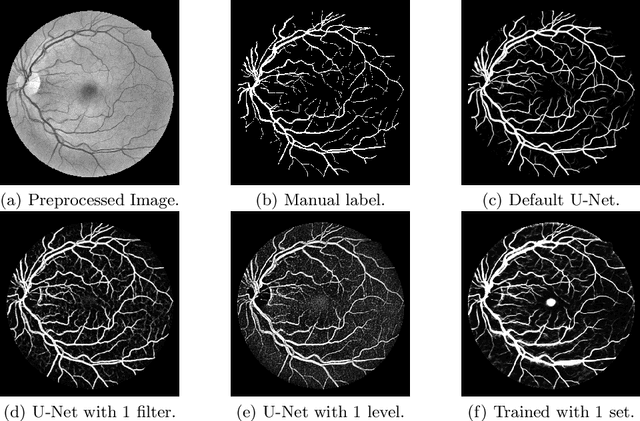
Retinal vessel segmentation is an essential step for fundus image analysis. With the recent advances of deep learning technologies, many convolutional neural networks have been applied in this field, including the successful U-Net. In this work, we firstly modify the U-Net with functional blocks aiming to pursue higher performance. The absence of the expected performance boost then lead us to dig into the opposite direction of shrinking the U-Net and exploring the extreme conditions such that its segmentation performance is maintained. Experiment series to simplify the network structure, reduce the network size and restrict the training conditions are designed. Results show that for retinal vessel segmentation on DRIVE database, U-Net does not degenerate until surprisingly acute conditions: one level, one filter in convolutional layers, and one training sample. This experimental discovery is both counter-intuitive and worthwhile. Not only are the extremes of the U-Net explored on a well-studied application, but also one intriguing warning is raised for the research methodology which seeks for marginal performance enhancement regardless of the resource cost.

Lesson Learnt: Modularization of Deep Networks Allow Cross-Modality Reuse

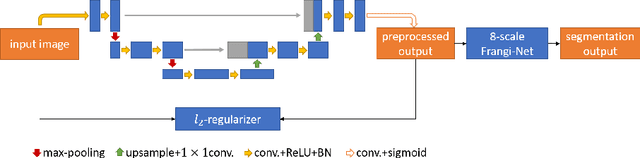
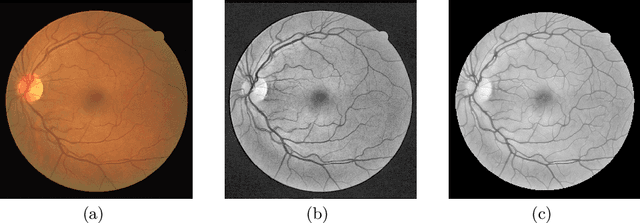
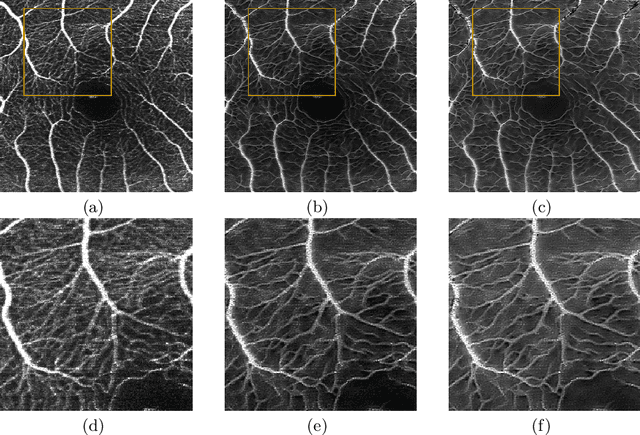
Fundus photography and Optical Coherence Tomography Angiography (OCT-A) are two commonly used modalities in ophthalmic imaging. With the development of deep learning algorithms, fundus image processing, especially retinal vessel segmentation, has been extensively studied. Built upon the known operator theory, interpretable deep network pipelines with well-defined modules have been constructed on fundus images. In this work, we firstly train a modularized network pipeline for the task of retinal vessel segmentation on the fundus database DRIVE. The pretrained preprocessing module from the pipeline is then directly transferred onto OCT-A data for image quality enhancement without further fine-tuning. Output images show that the preprocessing net can balance the contrast, suppress noise and thereby produce vessel trees with improved connectivity in both image modalities. The visual impression is confirmed by an observer study with five OCT-A experts. Statistics of the grades by the experts indicate that the transferred module improves both the image quality and the diagnostic quality. Our work provides an example that modules within network pipelines that are built upon the known operator theory facilitate cross-modality reuse without additional training or transfer learning.

A Divide-and-Conquer Approach towards Understanding Deep Networks

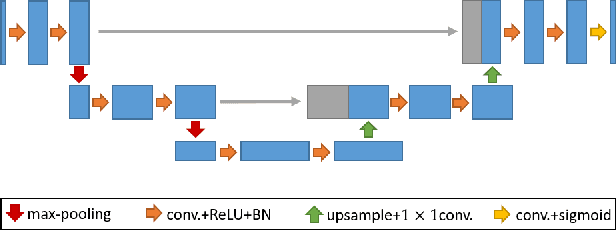
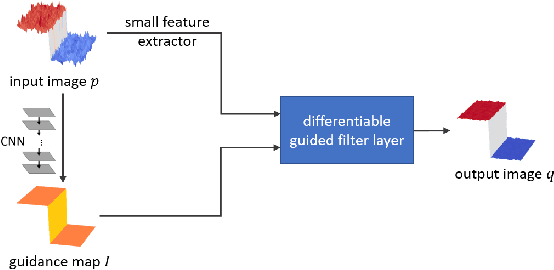
Deep neural networks have achieved tremendous success in various fields including medical image segmentation. However, they have long been criticized for being a black-box, in that interpretation, understanding and correcting architectures is difficult as there is no general theory for deep neural network design. Previously, precision learning was proposed to fuse deep architectures and traditional approaches. Deep networks constructed in this way benefit from the original known operator, have fewer parameters, and improved interpretability. However, they do not yield state-of-the-art performance in all applications. In this paper, we propose to analyze deep networks using known operators, by adopting a divide-and-conquer strategy to replace network components, whilst retaining its performance. The task of retinal vessel segmentation is investigated for this purpose. We start with a high-performance U-Net and show by step-by-step conversion that we are able to divide the network into modules of known operators. The results indicate that a combination of a trainable guided filter and a trainable version of the Frangi filter yields a performance at the level of U-Net (AUC 0.974 vs. 0.972) with a tremendous reduction in parameters (111,536 vs. 9,575). In addition, the trained layers can be mapped back into their original algorithmic interpretation and analyzed using standard tools of signal processing.

Learning with Known Operators reduces Maximum Training Error Bounds

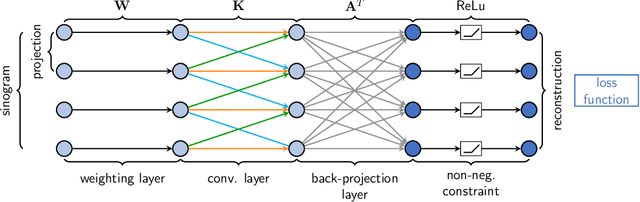
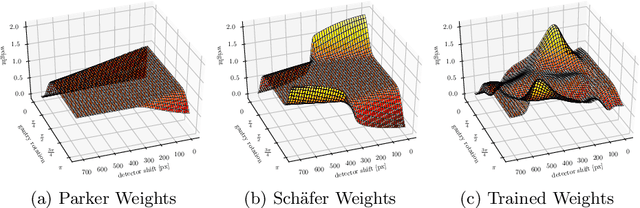
We describe an approach for incorporating prior knowledge into machine learning algorithms. We aim at applications in physics and signal processing in which we know that certain operations must be embedded into the algorithm. Any operation that allows computation of a gradient or sub-gradient towards its inputs is suited for our framework. We derive a maximal error bound for deep nets that demonstrates that inclusion of prior knowledge results in its reduction. Furthermore, we also show experimentally that known operators reduce the number of free parameters. We apply this approach to various tasks ranging from CT image reconstruction over vessel segmentation to the derivation of previously unknown imaging algorithms. As such the concept is widely applicable for many researchers in physics, imaging, and signal processing. We assume that our analysis will support further investigation of known operators in other fields of physics, imaging, and signal processing.

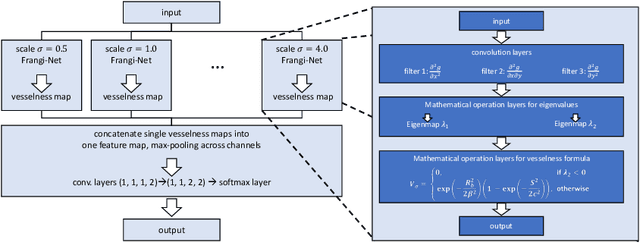
Frangi-Net: A Neural Network Approach to Vessel Segmentation

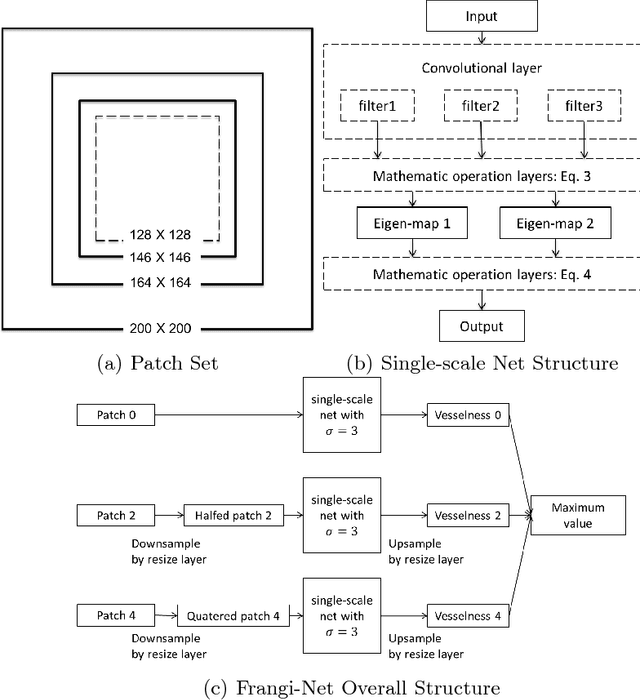
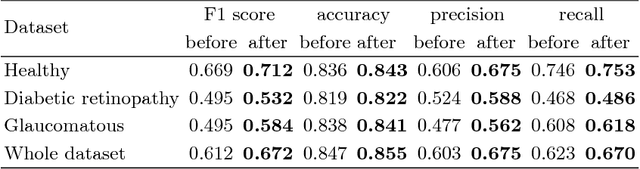
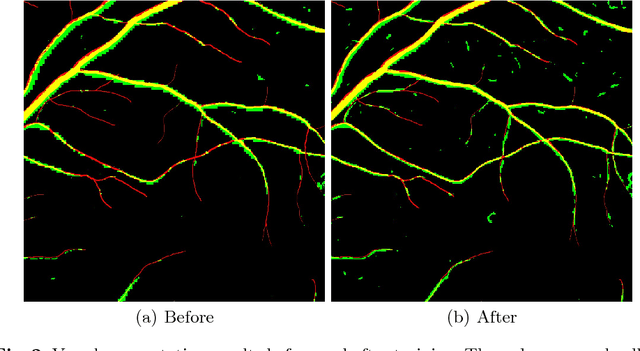
In this paper, we reformulate the conventional 2-D Frangi vesselness measure into a pre-weighted neural network ("Frangi-Net"), and illustrate that the Frangi-Net is equivalent to the original Frangi filter. Furthermore, we show that, as a neural network, Frangi-Net is trainable. We evaluate the proposed method on a set of 45 high resolution fundus images. After fine-tuning, we observe both qualitative and quantitative improvements in the segmentation quality compared to the original Frangi measure, with an increase up to $17\%$ in F1 score.