Learning with Known Operators reduces Maximum Training Error Bounds
Paper and Code
Jul 03, 2019
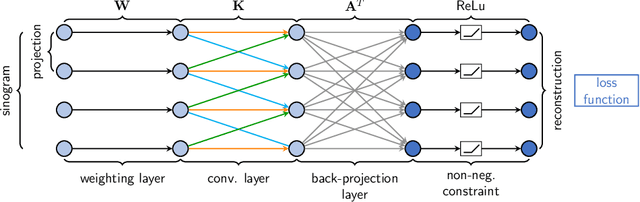
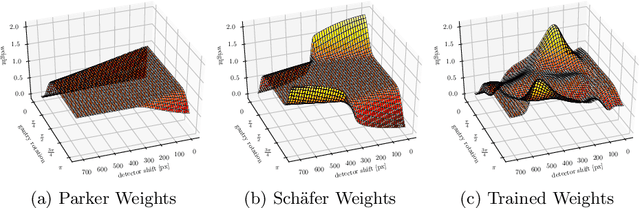
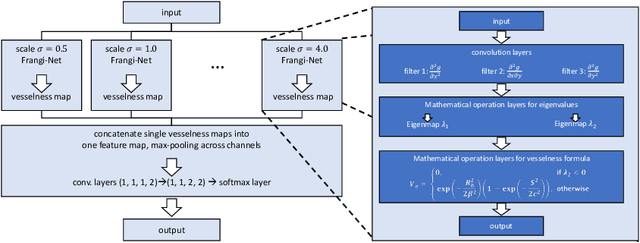
We describe an approach for incorporating prior knowledge into machine learning algorithms. We aim at applications in physics and signal processing in which we know that certain operations must be embedded into the algorithm. Any operation that allows computation of a gradient or sub-gradient towards its inputs is suited for our framework. We derive a maximal error bound for deep nets that demonstrates that inclusion of prior knowledge results in its reduction. Furthermore, we also show experimentally that known operators reduce the number of free parameters. We apply this approach to various tasks ranging from CT image reconstruction over vessel segmentation to the derivation of previously unknown imaging algorithms. As such the concept is widely applicable for many researchers in physics, imaging, and signal processing. We assume that our analysis will support further investigation of known operators in other fields of physics, imaging, and signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge