Lasse Kling
Synthetic Image Rendering Solves Annotation Problem in Deep Learning Nanoparticle Segmentation
Nov 20, 2020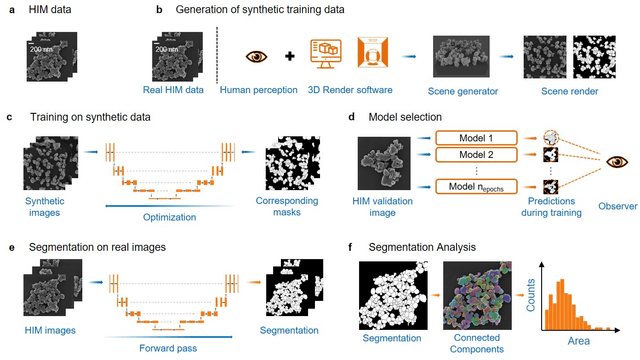
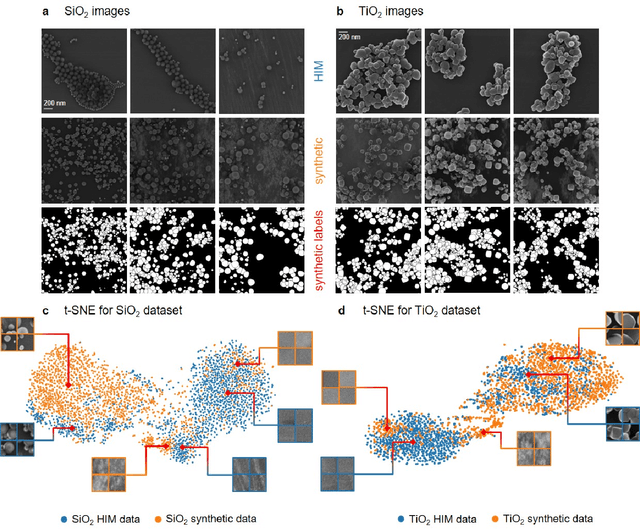
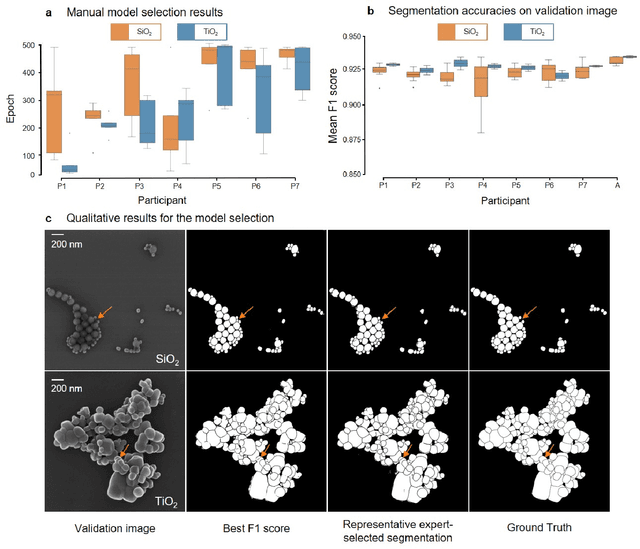
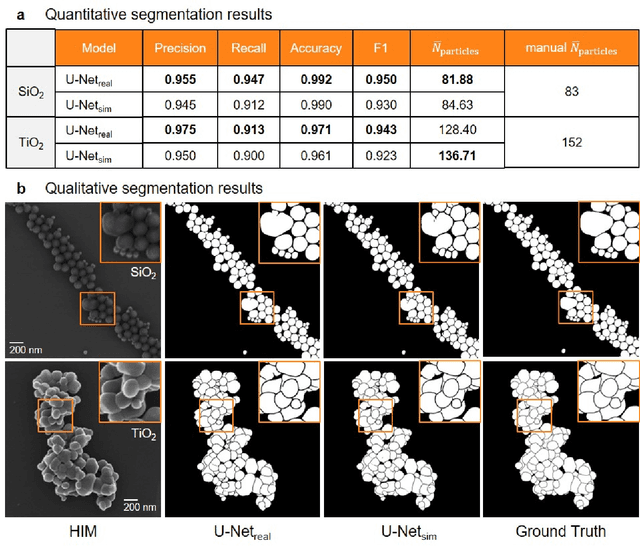
Abstract:Nanoparticles occur in various environments as a consequence of man-made processes, which raises concerns about their impact on the environment and human health. To allow for proper risk assessment, a precise and statistically relevant analysis of particle characteristics (such as e.g. size, shape and composition) is required that would greatly benefit from automated image analysis procedures. While deep learning shows impressive results in object detection tasks, its applicability is limited by the amount of representative, experimentally collected and manually annotated training data. Here, we present an elegant, flexible and versatile method to bypass this costly and tedious data acquisition process. We show that using a rendering software allows to generate realistic, synthetic training data to train a state-of-the art deep neural network. Using this approach, we derive a segmentation accuracy that is comparable to man-made annotations for toxicologically relevant metal-oxide nanoparticle ensembles which we chose as examples. Our study paves the way towards the use of deep learning for automated, high-throughput particle detection in a variety of imaging techniques such as microscopies and spectroscopies, for a wide variety of studies and applications, including the detection of plastic micro- and nanoparticles.
Learning with Known Operators reduces Maximum Training Error Bounds
Jul 03, 2019
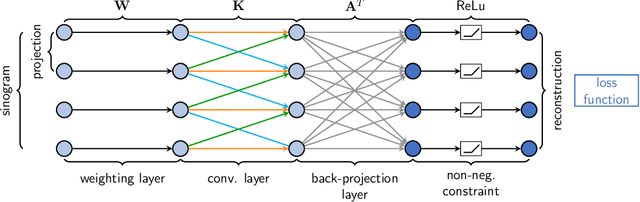
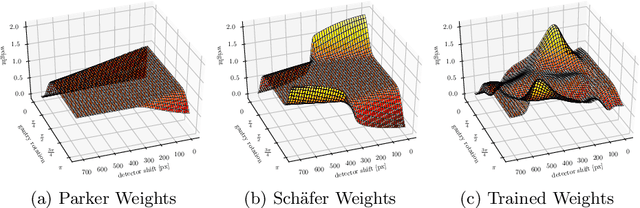
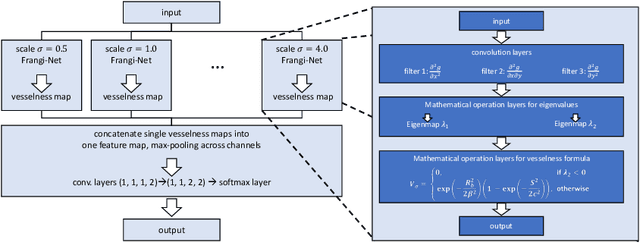
Abstract:We describe an approach for incorporating prior knowledge into machine learning algorithms. We aim at applications in physics and signal processing in which we know that certain operations must be embedded into the algorithm. Any operation that allows computation of a gradient or sub-gradient towards its inputs is suited for our framework. We derive a maximal error bound for deep nets that demonstrates that inclusion of prior knowledge results in its reduction. Furthermore, we also show experimentally that known operators reduce the number of free parameters. We apply this approach to various tasks ranging from CT image reconstruction over vessel segmentation to the derivation of previously unknown imaging algorithms. As such the concept is widely applicable for many researchers in physics, imaging, and signal processing. We assume that our analysis will support further investigation of known operators in other fields of physics, imaging, and signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge