Compensation based Dictionary Transfer for Similar Multispectral Image Spectral Super-resolution

Utilizing a spectral dictionary learned from a couple of similar-scene multi- and hyperspectral image, it is possible to reconstruct a desired hyperspectral image only with one single multispectral image. However, the differences between the similar scene and the desired hyperspectral image make it difficult to directly apply the spectral dictionary from the training domain to the task domain. To this end, a compensation matrix based dictionary transfer method for the similar-scene multispectral image spectral super-resolution is proposed in this paper, trying to reconstruct a more accurate high spatial resolution hyperspectral image. Specifically, a spectral dictionary transfer scheme is established by using a compensation matrix with similarity constraint, to transfer the spectral dictionary learned in the training domain to the spectral super-resolution domain. Subsequently, the sparse coefficient matrix is optimized under sparse and low-rank constraints. Experimental results on two AVIRIS datasets from different scenes indicate that, the proposed method outperforms other related SOTA methods.

Single-source Domain Expansion Network for Cross-Scene Hyperspectral Image Classification

Currently, cross-scene hyperspectral image (HSI) classification has drawn increasing attention. It is necessary to train a model only on source domain (SD) and directly transferring the model to target domain (TD), when TD needs to be processed in real time and cannot be reused for training. Based on the idea of domain generalization, a Single-source Domain Expansion Network (SDEnet) is developed to ensure the reliability and effectiveness of domain extension. The method uses generative adversarial learning to train in SD and test in TD. A generator including semantic encoder and morph encoder is designed to generate the extended domain (ED) based on encoder-randomization-decoder architecture, where spatial and spectral randomization are specifically used to generate variable spatial and spectral information, and the morphological knowledge is implicitly applied as domain invariant information during domain expansion. Furthermore, the supervised contrastive learning is employed in the discriminator to learn class-wise domain invariant representation, which drives intra-class samples of SD and ED. Meanwhile, adversarial training is designed to optimize the generator to drive intra-class samples of SD and ED to be separated. Extensive experiments on two public HSI datasets and one additional multispectral image (MSI) dataset demonstrate the superiority of the proposed method when compared with state-of-the-art techniques.

Fast UAV Trajectory Optimization using Bilevel Optimization with Analytical Gradients

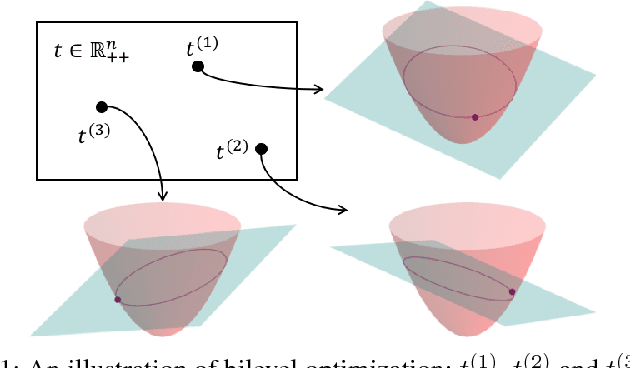
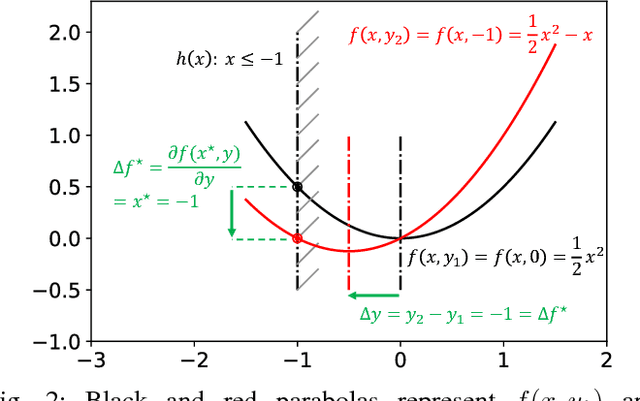
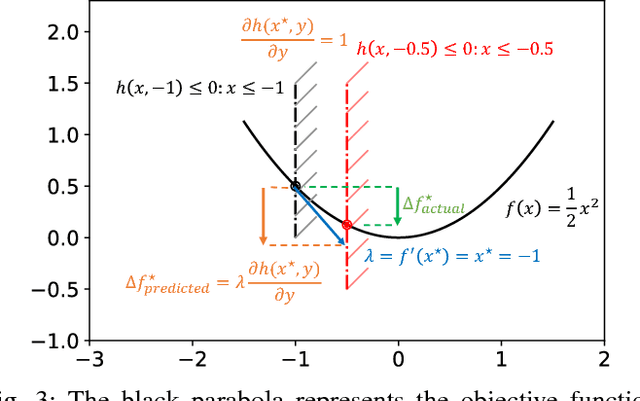
This paper presents an efficient optimization framework that solves trajectory optimization problems efficiently by decoupling state variables from timing variables, thereby decomposing a challenging nonlinear programming (NLP) problem into two easier subproblems. With timing fixed, the state variables can be optimized efficiently using convex optimization, and so the time variables can be optimized using a separate outer optimization. This is a bilevel optimization in which the outer objective function itself requires an optimization to compute. The challenge is that gradient optimization methods require the gradient of the objective function with respect to the time variables, which is not available. Whereas the finite difference method must solve many optimization problems to compute a gradient, this paper proposes a more efficient method: the dual solution (Lagrange multipliers) of the convex optimization problem is exploited to calculate the analytical gradient. Since the dual solution is a by-product of the convex optimization problem, the gradient can be obtained `for free' with high accuracy. The framework is demonstrated on solving minimum-jerk trajectory optimization problems in safety corridors for unmanned aerial vehicles (UAVs). Experiments demonstrate that bilevel optimization improves performance over a standard NLP solver, and analytical gradients outperforms finite differences. With a 40\,ms cutoff time, our approach achieves over 8 times better suboptimality than the current state-of-the-art.