Fast UAV Trajectory Optimization using Bilevel Optimization with Analytical Gradients

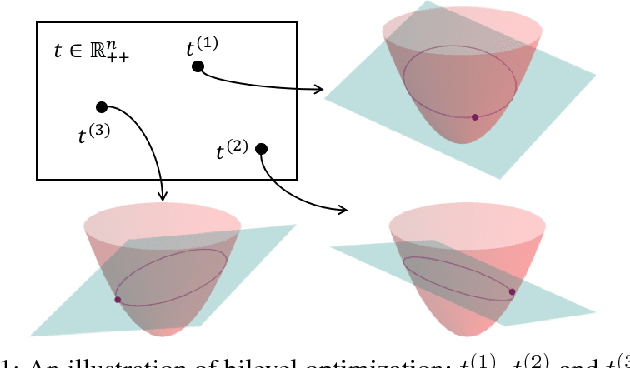
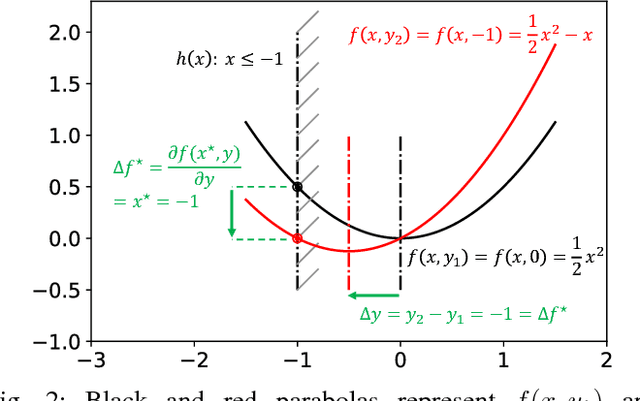
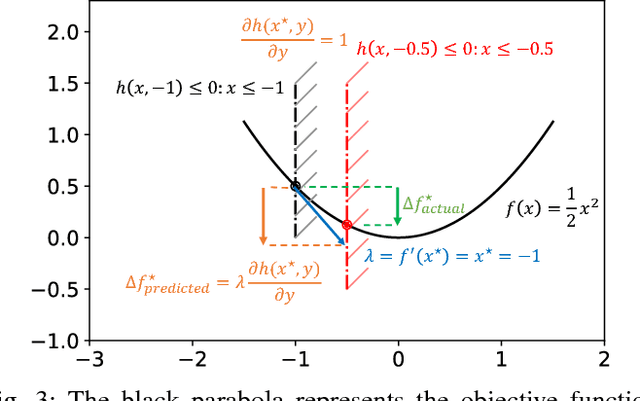
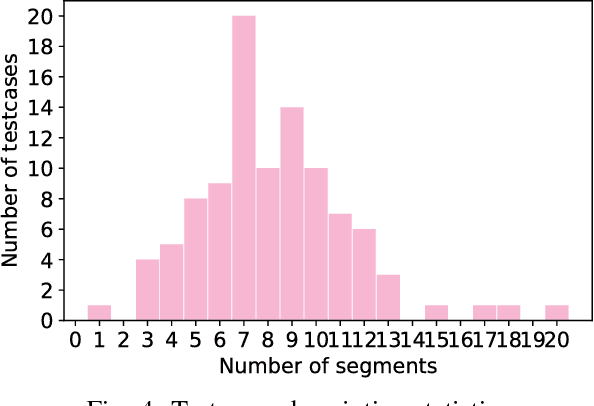
This paper presents an efficient optimization framework that solves trajectory optimization problems efficiently by decoupling state variables from timing variables, thereby decomposing a challenging nonlinear programming (NLP) problem into two easier subproblems. With timing fixed, the state variables can be optimized efficiently using convex optimization, and so the time variables can be optimized using a separate outer optimization. This is a bilevel optimization in which the outer objective function itself requires an optimization to compute. The challenge is that gradient optimization methods require the gradient of the objective function with respect to the time variables, which is not available. Whereas the finite difference method must solve many optimization problems to compute a gradient, this paper proposes a more efficient method: the dual solution (Lagrange multipliers) of the convex optimization problem is exploited to calculate the analytical gradient. Since the dual solution is a by-product of the convex optimization problem, the gradient can be obtained `for free' with high accuracy. The framework is demonstrated on solving minimum-jerk trajectory optimization problems in safety corridors for unmanned aerial vehicles (UAVs). Experiments demonstrate that bilevel optimization improves performance over a standard NLP solver, and analytical gradients outperforms finite differences. With a 40\,ms cutoff time, our approach achieves over 8 times better suboptimality than the current state-of-the-art.