Toward Autonomous Robotic Micro-Suturing using Optical Coherence Tomography Calibration and Path Planning

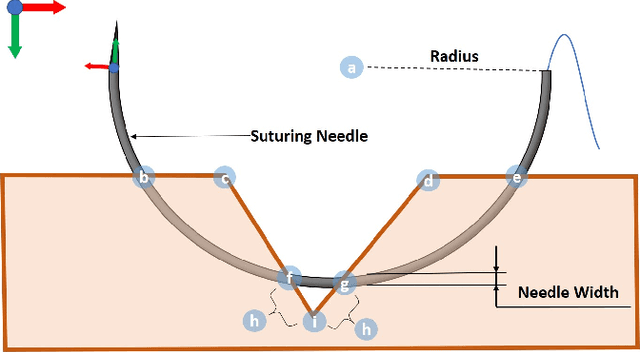
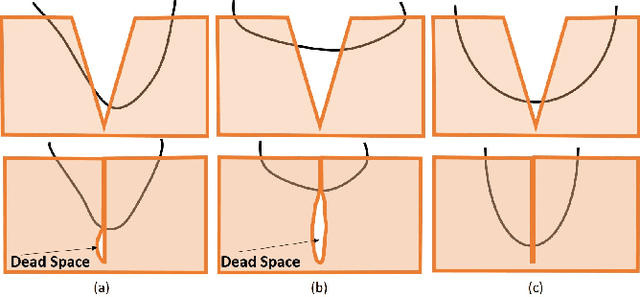
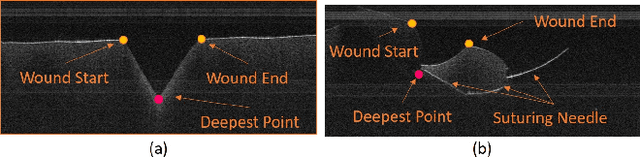
Robotic automation has the potential to assist human surgeons in performing suturing tasks in microsurgery, and in order to do so a robot must be able to guide a needle with sub-millimeter precision through soft tissue. This paper presents a robotic suturing system that uses 3D optical coherence tomography (OCT) system for imaging feedback. Calibration of the robot-OCT and robot-needle transforms, wound detection, keypoint identification, and path planning are all performed automatically. The calibration method handles pose uncertainty when the needle is grasped using a variant of iterative closest points. The path planner uses the identified wound shape to calculate needle entry and exit points to yield an evenly-matched wound shape after closure. Experiments on tissue phantoms and animal tissue demonstrate that the system can pass a suture needle through wounds with 0.27 mm overall accuracy in achieving the planned entry and exit points.

Fast UAV Trajectory Optimization using Bilevel Optimization with Analytical Gradients

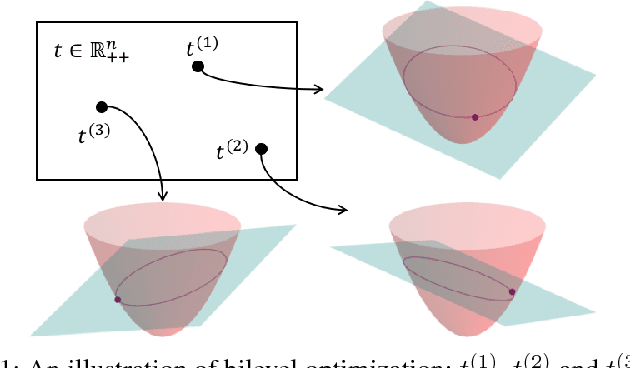
This paper presents an efficient optimization framework that solves trajectory optimization problems efficiently by decoupling state variables from timing variables, thereby decomposing a challenging nonlinear programming (NLP) problem into two easier subproblems. With timing fixed, the state variables can be optimized efficiently using convex optimization, and so the time variables can be optimized using a separate outer optimization. This is a bilevel optimization in which the outer objective function itself requires an optimization to compute. The challenge is that gradient optimization methods require the gradient of the objective function with respect to the time variables, which is not available. Whereas the finite difference method must solve many optimization problems to compute a gradient, this paper proposes a more efficient method: the dual solution (Lagrange multipliers) of the convex optimization problem is exploited to calculate the analytical gradient. Since the dual solution is a by-product of the convex optimization problem, the gradient can be obtained `for free' with high accuracy. The framework is demonstrated on solving minimum-jerk trajectory optimization problems in safety corridors for unmanned aerial vehicles (UAVs). Experiments demonstrate that bilevel optimization improves performance over a standard NLP solver, and analytical gradients outperforms finite differences. With a 40\,ms cutoff time, our approach achieves over 8 times better suboptimality than the current state-of-the-art.

Discontinuity-Sensitive Optimal Control Learning by Mixture of Experts

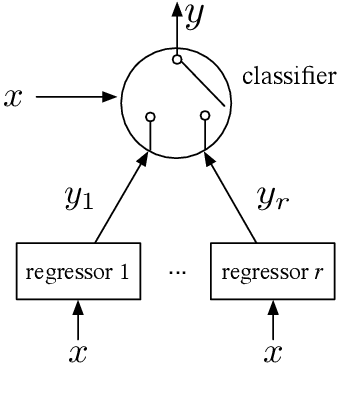
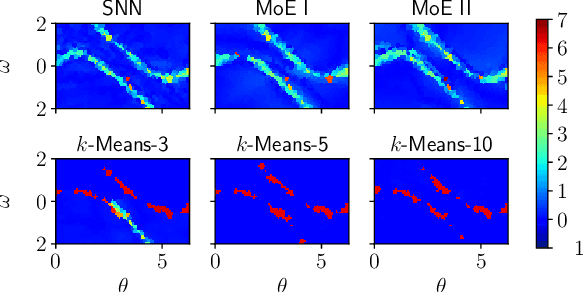
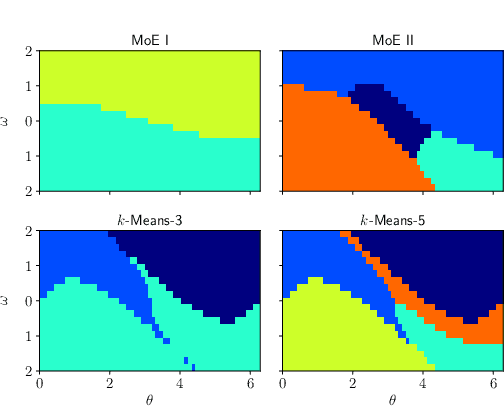
This paper proposes a discontinuity-sensitive approach to learn the solutions of parametric optimal control problems with high accuracy. Many tasks, ranging from model predictive control to reinforcement learning, may be solved by learning optimal solutions as a function of problem parameters. However, nonconvexity, discrete homotopy classes, and control switching cause discontinuity in the parameter-solution mapping, thus making learning difficult for traditional continuous function approximators. A mixture of experts (MoE) model composed of a classifier and several regressors is proposed to address such an issue. The optimal trajectories of different parameters are clustered such that in each cluster the trajectories are continuous function of problem parameters. Numerical examples on benchmark problems show that training the classifier and regressors individually outperforms joint training of MoE. With suitably chosen clusters, this approach not only achieves lower prediction error with less training data and fewer model parameters, but also leads to dramatic improvements in the reliability of trajectory tracking compared to traditional universal function approximation models (e.g., neural networks).