Discontinuity-Sensitive Optimal Control Learning by Mixture of Experts
Paper and Code
Mar 07, 2018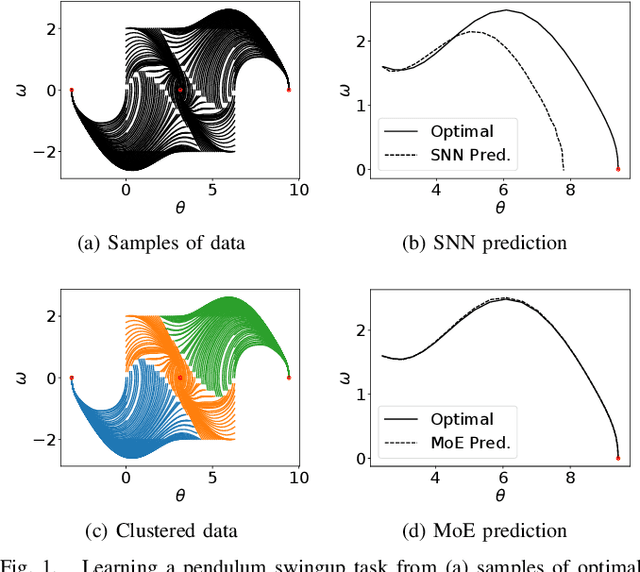
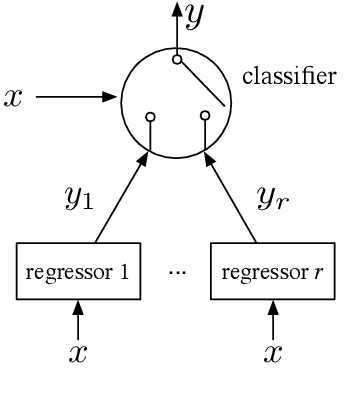
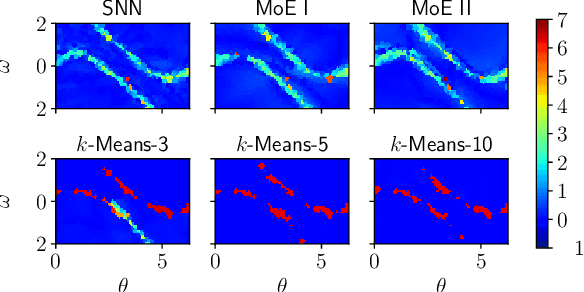
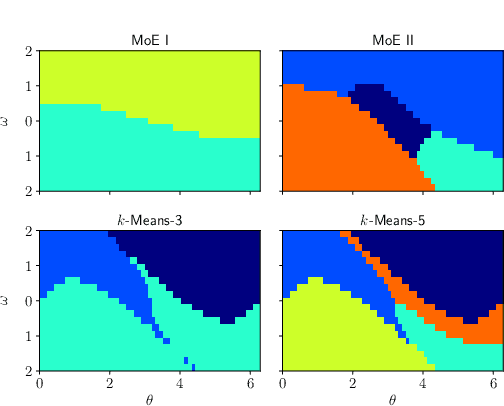
This paper proposes a discontinuity-sensitive approach to learn the solutions of parametric optimal control problems with high accuracy. Many tasks, ranging from model predictive control to reinforcement learning, may be solved by learning optimal solutions as a function of problem parameters. However, nonconvexity, discrete homotopy classes, and control switching cause discontinuity in the parameter-solution mapping, thus making learning difficult for traditional continuous function approximators. A mixture of experts (MoE) model composed of a classifier and several regressors is proposed to address such an issue. The optimal trajectories of different parameters are clustered such that in each cluster the trajectories are continuous function of problem parameters. Numerical examples on benchmark problems show that training the classifier and regressors individually outperforms joint training of MoE. With suitably chosen clusters, this approach not only achieves lower prediction error with less training data and fewer model parameters, but also leads to dramatic improvements in the reliability of trajectory tracking compared to traditional universal function approximation models (e.g., neural networks).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge