Wanwei Liu
UR4NNV: Neural Network Verification, Under-approximation Reachability Works!
Jan 23, 2024Abstract:Recently, formal verification of deep neural networks (DNNs) has garnered considerable attention, and over-approximation based methods have become popular due to their effectiveness and efficiency. However, these strategies face challenges in addressing the "unknown dilemma" concerning whether the exact output region or the introduced approximation error violates the property in question. To address this, this paper introduces the UR4NNV verification framework, which utilizes under-approximation reachability analysis for DNN verification for the first time. UR4NNV focuses on DNNs with Rectified Linear Unit (ReLU) activations and employs a binary tree branch-based under-approximation algorithm. In each epoch, UR4NNV under-approximates a sub-polytope of the reachable set and verifies this polytope against the given property. Through a trial-and-error approach, UR4NNV effectively falsifies DNN properties while providing confidence levels when reaching verification epoch bounds and failing falsifying properties. Experimental comparisons with existing verification methods demonstrate the effectiveness and efficiency of UR4NNV, significantly reducing the impact of the "unknown dilemma".
An Automata-Theoretic Approach to Synthesizing Binarized Neural Networks
Jul 29, 2023Abstract:Deep neural networks, (DNNs, a.k.a. NNs), have been widely used in various tasks and have been proven to be successful. However, the accompanied expensive computing and storage costs make the deployments in resource-constrained devices a significant concern. To solve this issue, quantization has emerged as an effective way to reduce the costs of DNNs with little accuracy degradation by quantizing floating-point numbers to low-width fixed-point representations. Quantized neural networks (QNNs) have been developed, with binarized neural networks (BNNs) restricted to binary values as a special case. Another concern about neural networks is their vulnerability and lack of interpretability. Despite the active research on trustworthy of DNNs, few approaches have been proposed to QNNs. To this end, this paper presents an automata-theoretic approach to synthesizing BNNs that meet designated properties. More specifically, we define a temporal logic, called BLTL, as the specification language. We show that each BLTL formula can be transformed into an automaton on finite words. To deal with the state-explosion problem, we provide a tableau-based approach in real implementation. For the synthesis procedure, we utilize SMT solvers to detect the existence of a model (i.e., a BNN) in the construction process. Notably, synthesis provides a way to determine the hyper-parameters of the network before training.Moreover, we experimentally evaluate our approach and demonstrate its effectiveness in improving the individual fairness and local robustness of BNNs while maintaining accuracy to a great extent.
Verifying Safety of Neural Networks from Topological Perspectives
Jun 27, 2023Abstract:Neural networks (NNs) are increasingly applied in safety-critical systems such as autonomous vehicles. However, they are fragile and are often ill-behaved. Consequently, their behaviors should undergo rigorous guarantees before deployment in practice. In this paper, we propose a set-boundary reachability method to investigate the safety verification problem of NNs from a topological perspective. Given an NN with an input set and a safe set, the safety verification problem is to determine whether all outputs of the NN resulting from the input set fall within the safe set. In our method, the homeomorphism property and the open map property of NNs are mainly exploited, which establish rigorous guarantees between the boundaries of the input set and the boundaries of the output set. The exploitation of these two properties facilitates reachability computations via extracting subsets of the input set rather than the entire input set, thus controlling the wrapping effect in reachability analysis and facilitating the reduction of computation burdens for safety verification. The homeomorphism property exists in some widely used NNs such as invertible residual networks (i-ResNets) and Neural ordinary differential equations (Neural ODEs), and the open map is a less strict property and easier to satisfy compared with the homeomorphism property. For NNs establishing either of these properties, our set-boundary reachability method only needs to perform reachability analysis on the boundary of the input set. Moreover, for NNs that do not feature these properties with respect to the input set, we explore subsets of the input set for establishing the local homeomorphism property and then abandon these subsets for reachability computations. Finally, some examples demonstrate the performance of the proposed method.
Repairing Deep Neural Networks Based on Behavior Imitation
May 05, 2023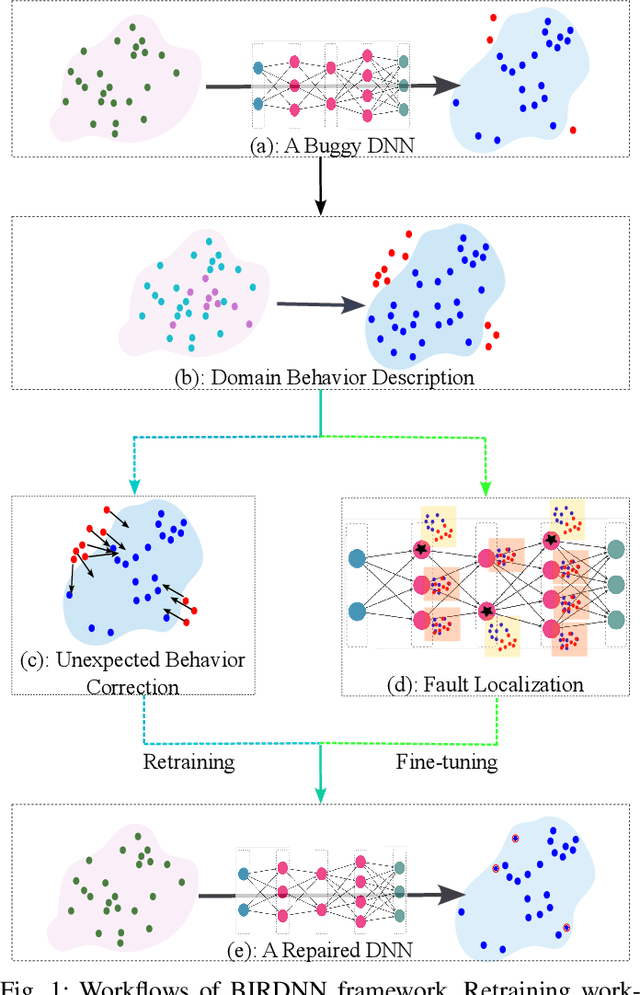
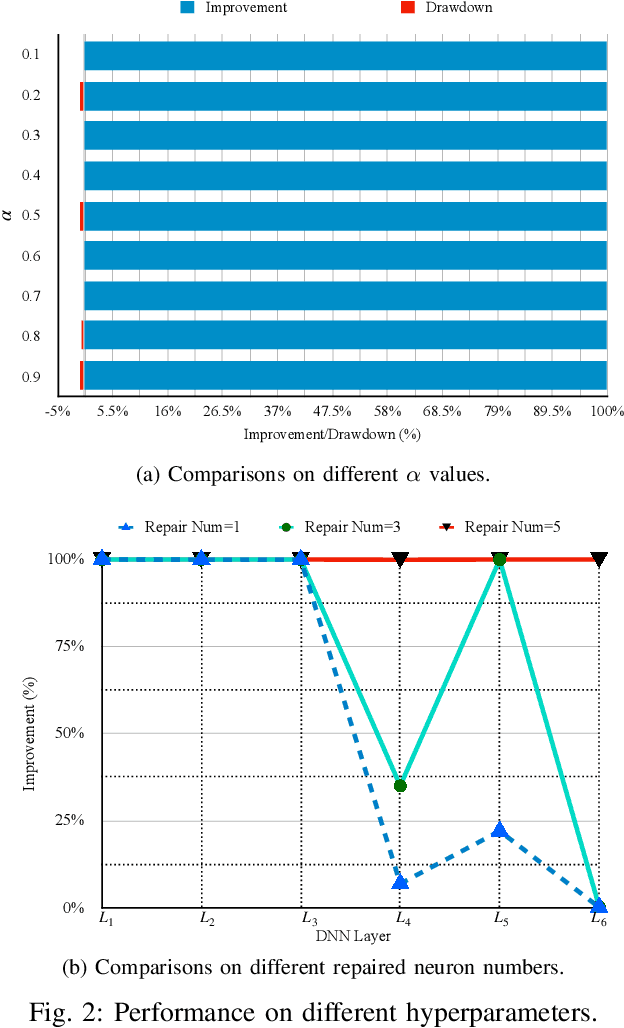
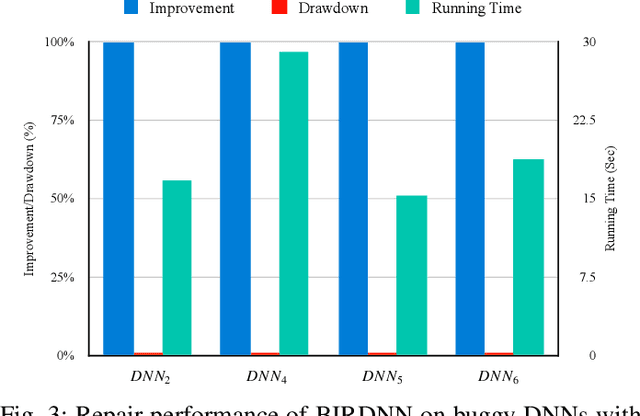
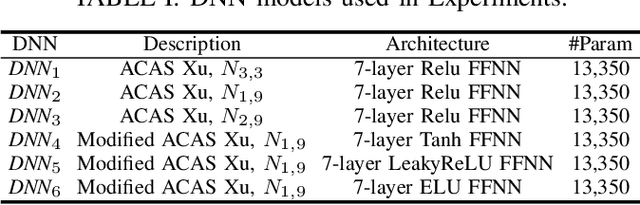
Abstract:The increasing use of deep neural networks (DNNs) in safety-critical systems has raised concerns about their potential for exhibiting ill-behaviors. While DNN verification and testing provide post hoc conclusions regarding unexpected behaviors, they do not prevent the erroneous behaviors from occurring. To address this issue, DNN repair/patch aims to eliminate unexpected predictions generated by defective DNNs. Two typical DNN repair paradigms are retraining and fine-tuning. However, existing methods focus on the high-level abstract interpretation or inference of state spaces, ignoring the underlying neurons' outputs. This renders patch processes computationally prohibitive and limited to piecewise linear (PWL) activation functions to great extent. To address these shortcomings, we propose a behavior-imitation based repair framework, BIRDNN, which integrates the two repair paradigms for the first time. BIRDNN corrects incorrect predictions of negative samples by imitating the closest expected behaviors of positive samples during the retraining repair procedure. For the fine-tuning repair process, BIRDNN analyzes the behavior differences of neurons on positive and negative samples to identify the most responsible neurons for the erroneous behaviors. To tackle more challenging domain-wise repair problems (DRPs), we synthesize BIRDNN with a domain behavior characterization technique to repair buggy DNNs in a probably approximated correct style. We also implement a prototype tool based on BIRDNN and evaluate it on ACAS Xu DNNs. Our experimental results show that BIRDNN can successfully repair buggy DNNs with significantly higher efficiency than state-of-the-art repair tools. Additionally, BIRDNN is highly compatible with different activation functions.
Credit Assignment for Trained Neural Networks Based on Koopman Operator Theory
Dec 02, 2022Abstract:Credit assignment problem of neural networks refers to evaluating the credit of each network component to the final outputs. For an untrained neural network, approaches to tackling it have made great contributions to parameter update and model revolution during the training phase. This problem on trained neural networks receives rare attention, nevertheless, it plays an increasingly important role in neural network patch, specification and verification. Based on Koopman operator theory, this paper presents an alternative perspective of linear dynamics on dealing with the credit assignment problem for trained neural networks. Regarding a neural network as the composition of sub-dynamics series, we utilize step-delay embedding to capture snapshots of each component, characterizing the established mapping as exactly as possible. To circumvent the dimension-difference problem encountered during the embedding, a composition and decomposition of an auxiliary linear layer, termed minimal linear dimension alignment, is carefully designed with rigorous formal guarantee. Afterwards, each component is approximated by a Koopman operator and we derive the Jacobian matrix and its corresponding determinant, similar to backward propagation. Then, we can define a metric with algebraic interpretability for the credit assignment of each network component. Moreover, experiments conducted on typical neural networks demonstrate the effectiveness of the proposed method.
Safety Verification for Neural Networks Based on Set-boundary Analysis
Oct 09, 2022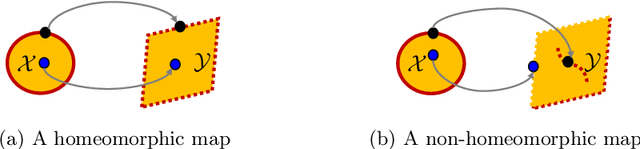
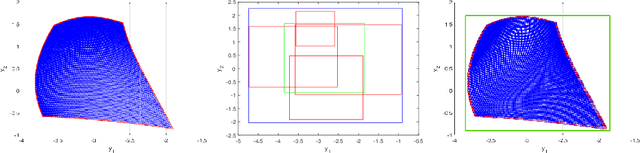
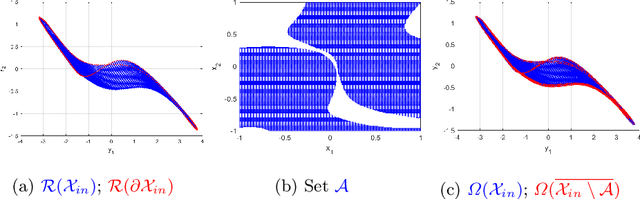

Abstract:Neural networks (NNs) are increasingly applied in safety-critical systems such as autonomous vehicles. However, they are fragile and are often ill-behaved. Consequently, their behaviors should undergo rigorous guarantees before deployment in practice. In this paper we propose a set-boundary reachability method to investigate the safety verification problem of NNs from a topological perspective. Given an NN with an input set and a safe set, the safety verification problem is to determine whether all outputs of the NN resulting from the input set fall within the safe set. In our method, the homeomorphism property of NNs is mainly exploited, which establishes a relationship mapping boundaries to boundaries. The exploitation of this property facilitates reachability computations via extracting subsets of the input set rather than the entire input set, thus controlling the wrapping effect in reachability analysis and facilitating the reduction of computation burdens for safety verification. The homeomorphism property exists in some widely used NNs such as invertible NNs. Notable representations are invertible residual networks (i-ResNets) and Neural ordinary differential equations (Neural ODEs). For these NNs, our set-boundary reachability method only needs to perform reachability analysis on the boundary of the input set. For NNs which do not feature this property with respect to the input set, we explore subsets of the input set for establishing the local homeomorphism property, and then abandon these subsets for reachability computations. Finally, some examples demonstrate the performance of the proposed method.
On the Properties of Kullback-Leibler Divergence Between Gaussians
Feb 24, 2021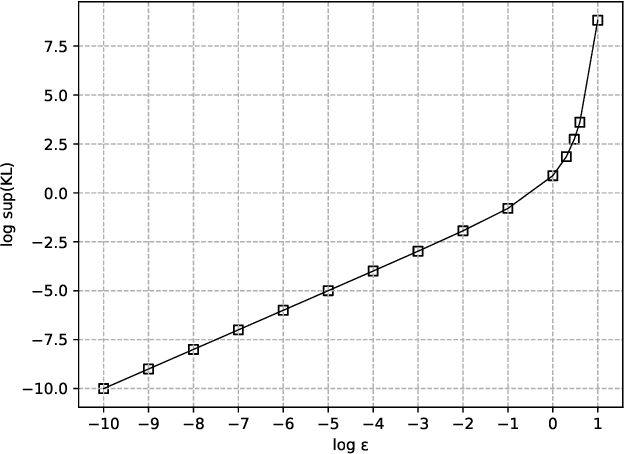
Abstract:Kullback-Leibler (KL) divergence is one of the most important divergence measures between probability distributions. In this paper, we investigate the properties of KL divergence between Gaussians. Firstly, for any two $n$-dimensional Gaussians $\mathcal{N}_1$ and $\mathcal{N}_2$, we find the supremum of $KL(\mathcal{N}_1||\mathcal{N}_2)$ when $KL(\mathcal{N}_2||\mathcal{N}_1)\leq \epsilon$ for $\epsilon>0$. This reveals the approximate symmetry of small KL divergence between Gaussians. We also find the infimum of $KL(\mathcal{N}_1||\mathcal{N}_2)$ when $KL(\mathcal{N}_2||\mathcal{N}_1)\geq M$ for $M>0$. Secondly, for any three $n$-dimensional Gaussians $\mathcal{N}_1, \mathcal{N}_2$ and $\mathcal{N}_3$, we find a bound of $KL(\mathcal{N}_1||\mathcal{N}_3)$ if $KL(\mathcal{N}_1||\mathcal{N}_2)$ and $KL(\mathcal{N}_2||\mathcal{N}_3)$ are bounded. This reveals that the KL divergence between Gaussians follows a relaxed triangle inequality. Importantly, all the bounds in the theorems presented in this paper are independent of the dimension $n$.
On Sufficient and Necessary Conditions in Bounded CTL
Mar 13, 2020
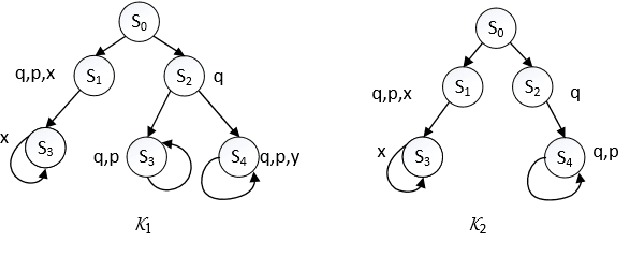

Abstract:Computation Tree Logic (CTL) is one of the central formalisms in formal verification. As a specification language, it is used to express a property that the system at hand is expected to satisfy. From both the verification and the system design points of view, some information content of such property might become irrelevant for the system due to various reasons e.g., it might become obsolete by time, or perhaps infeasible due to practical difficulties. Then, the problem arises on how to subtract such piece of information without altering the relevant system behaviour or violating the existing specifications. Moreover, in such a scenario, two crucial notions are informative: the strongest necessary condition (SNC) and the weakest sufficient condition (WSC) of a given property. To address such a scenario in a principled way, we introduce a forgetting-based approach in CTL and show that it can be used to compute SNC and WSC of a property under a given model. We study its theoretical properties and also show that our notion of forgetting satisfies existing essential postulates. Furthermore, we analyse the computational complexity of basic tasks, including various results for the relevant fragment CTLAF.
Out-of-Distribution Detection with Distance Guarantee in Deep Generative Models
Feb 09, 2020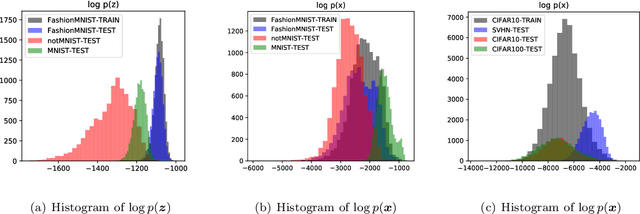
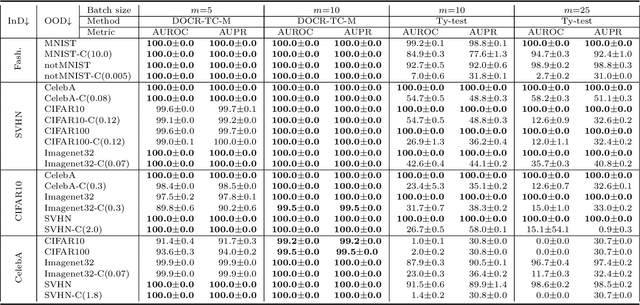
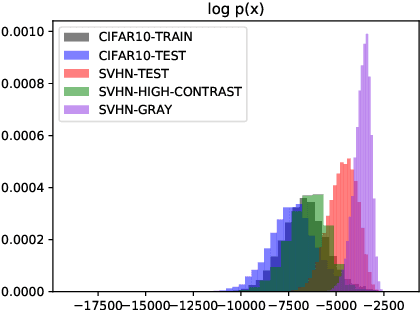
Abstract:Recent research has shown that it is challenging to detect out-of-distribution (OOD) data in deep generative models including flow-based models and variational autoencoders (VAEs). In this paper, we prove a theorem that, for a well-trained flow-based model, the distance between the distribution of representations of an OOD dataset and prior can be large enough, as long as the distance between the distributions of the training dataset and the OOD dataset is large enough. Furthermore, our observation shows that, for flow-based model and VAE with factorized prior, the representations of OOD datasets are more correlated than that of the training dataset. Based on our theorem and observation, we propose detecting OOD data according to the total correlation of representations in flow-based model and VAE. Experimental results show that our method can achieve nearly 100\% AUROC for all the widely used benchmarks and has robustness against data manipulation. While the state-of-the-art method performs not better than random guessing for challenging problems and can be fooled by data manipulation in almost all cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge