On the Properties of Kullback-Leibler Divergence Between Gaussians

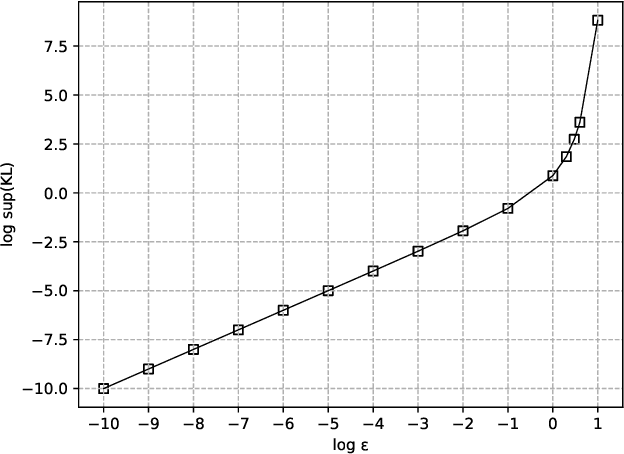
Kullback-Leibler (KL) divergence is one of the most important divergence measures between probability distributions. In this paper, we investigate the properties of KL divergence between Gaussians. Firstly, for any two $n$-dimensional Gaussians $\mathcal{N}_1$ and $\mathcal{N}_2$, we find the supremum of $KL(\mathcal{N}_1||\mathcal{N}_2)$ when $KL(\mathcal{N}_2||\mathcal{N}_1)\leq \epsilon$ for $\epsilon>0$. This reveals the approximate symmetry of small KL divergence between Gaussians. We also find the infimum of $KL(\mathcal{N}_1||\mathcal{N}_2)$ when $KL(\mathcal{N}_2||\mathcal{N}_1)\geq M$ for $M>0$. Secondly, for any three $n$-dimensional Gaussians $\mathcal{N}_1, \mathcal{N}_2$ and $\mathcal{N}_3$, we find a bound of $KL(\mathcal{N}_1||\mathcal{N}_3)$ if $KL(\mathcal{N}_1||\mathcal{N}_2)$ and $KL(\mathcal{N}_2||\mathcal{N}_3)$ are bounded. This reveals that the KL divergence between Gaussians follows a relaxed triangle inequality. Importantly, all the bounds in the theorems presented in this paper are independent of the dimension $n$.

Out-of-Distribution Detection with Distance Guarantee in Deep Generative Models

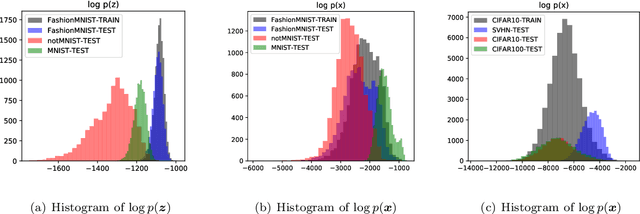
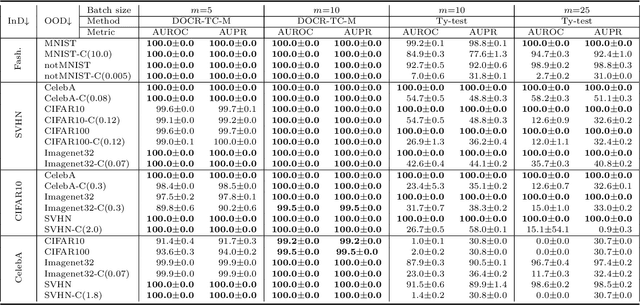
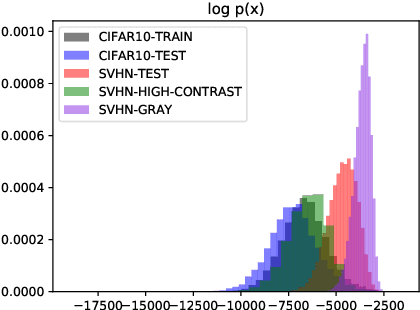
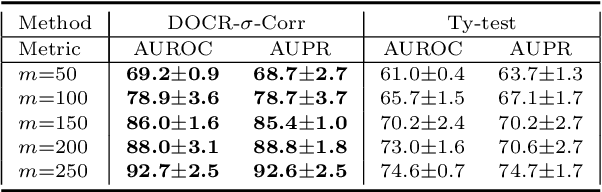
Recent research has shown that it is challenging to detect out-of-distribution (OOD) data in deep generative models including flow-based models and variational autoencoders (VAEs). In this paper, we prove a theorem that, for a well-trained flow-based model, the distance between the distribution of representations of an OOD dataset and prior can be large enough, as long as the distance between the distributions of the training dataset and the OOD dataset is large enough. Furthermore, our observation shows that, for flow-based model and VAE with factorized prior, the representations of OOD datasets are more correlated than that of the training dataset. Based on our theorem and observation, we propose detecting OOD data according to the total correlation of representations in flow-based model and VAE. Experimental results show that our method can achieve nearly 100\% AUROC for all the widely used benchmarks and has robustness against data manipulation. While the state-of-the-art method performs not better than random guessing for challenging problems and can be fooled by data manipulation in almost all cases.

Boosting the Robustness Verification of DNN by Identifying the Achilles's Heel

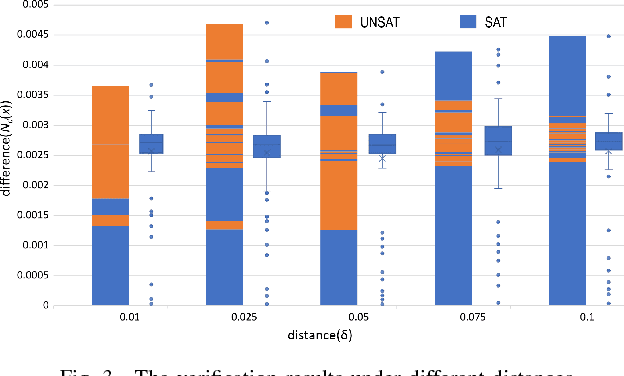
Deep Neural Network (DNN) is a widely used deep learning technique. How to ensure the safety of DNN-based system is a critical problem for the research and application of DNN. Robustness is an important safety property of DNN. However, existing work of verifying DNN's robustness is time-consuming and hard to scale to large-scale DNNs. In this paper, we propose a boosting method for DNN robustness verification, aiming to find counter-examples earlier. Our observation is DNN's different inputs have different possibilities of existing counter-examples around them, and the input with a small difference between the largest output value and the second largest output value tends to be the achilles's heel of the DNN. We have implemented our method and applied it on Reluplex, a state-of-the-art DNN verification tool, and four DNN attacking methods. The results of the extensive experiments on two benchmarks indicate the effectiveness of our boosting method.