UR4NNV: Neural Network Verification, Under-approximation Reachability Works!

Recently, formal verification of deep neural networks (DNNs) has garnered considerable attention, and over-approximation based methods have become popular due to their effectiveness and efficiency. However, these strategies face challenges in addressing the "unknown dilemma" concerning whether the exact output region or the introduced approximation error violates the property in question. To address this, this paper introduces the UR4NNV verification framework, which utilizes under-approximation reachability analysis for DNN verification for the first time. UR4NNV focuses on DNNs with Rectified Linear Unit (ReLU) activations and employs a binary tree branch-based under-approximation algorithm. In each epoch, UR4NNV under-approximates a sub-polytope of the reachable set and verifies this polytope against the given property. Through a trial-and-error approach, UR4NNV effectively falsifies DNN properties while providing confidence levels when reaching verification epoch bounds and failing falsifying properties. Experimental comparisons with existing verification methods demonstrate the effectiveness and efficiency of UR4NNV, significantly reducing the impact of the "unknown dilemma".

Verifying Safety of Neural Networks from Topological Perspectives

Neural networks (NNs) are increasingly applied in safety-critical systems such as autonomous vehicles. However, they are fragile and are often ill-behaved. Consequently, their behaviors should undergo rigorous guarantees before deployment in practice. In this paper, we propose a set-boundary reachability method to investigate the safety verification problem of NNs from a topological perspective. Given an NN with an input set and a safe set, the safety verification problem is to determine whether all outputs of the NN resulting from the input set fall within the safe set. In our method, the homeomorphism property and the open map property of NNs are mainly exploited, which establish rigorous guarantees between the boundaries of the input set and the boundaries of the output set. The exploitation of these two properties facilitates reachability computations via extracting subsets of the input set rather than the entire input set, thus controlling the wrapping effect in reachability analysis and facilitating the reduction of computation burdens for safety verification. The homeomorphism property exists in some widely used NNs such as invertible residual networks (i-ResNets) and Neural ordinary differential equations (Neural ODEs), and the open map is a less strict property and easier to satisfy compared with the homeomorphism property. For NNs establishing either of these properties, our set-boundary reachability method only needs to perform reachability analysis on the boundary of the input set. Moreover, for NNs that do not feature these properties with respect to the input set, we explore subsets of the input set for establishing the local homeomorphism property and then abandon these subsets for reachability computations. Finally, some examples demonstrate the performance of the proposed method.

Repairing Deep Neural Networks Based on Behavior Imitation

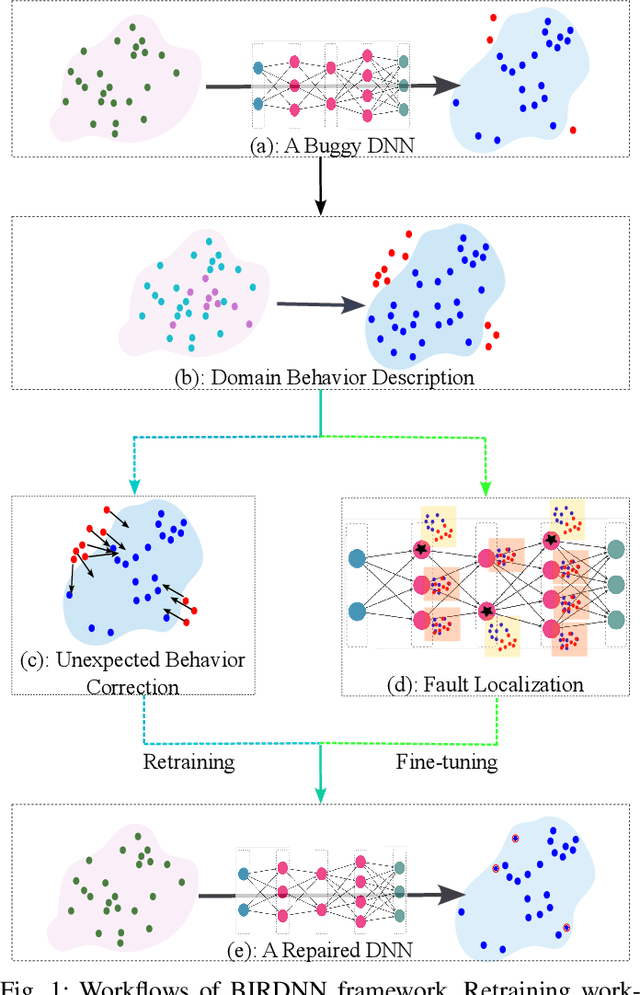
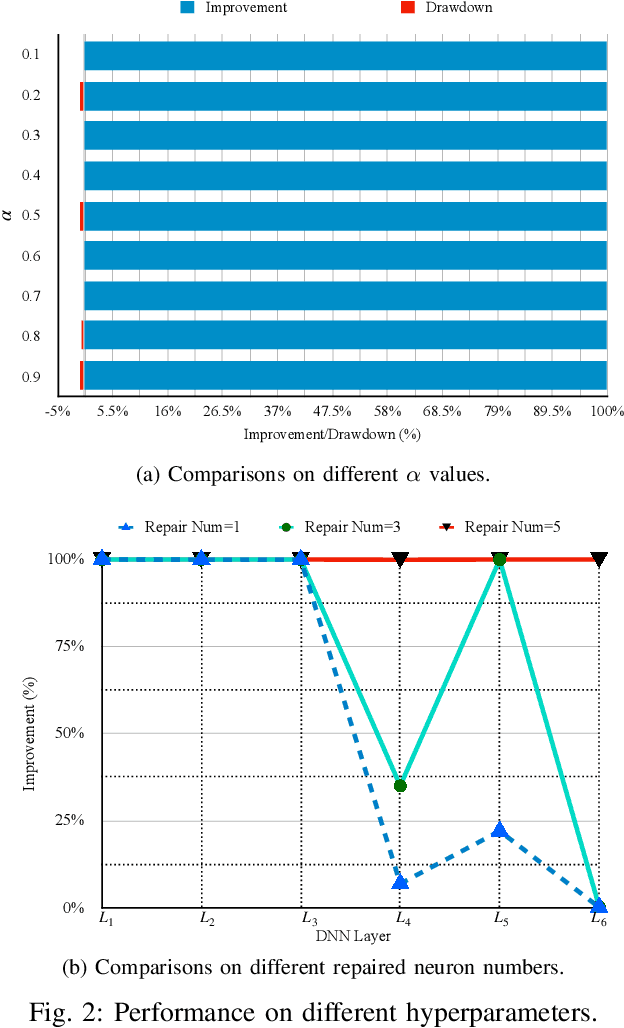
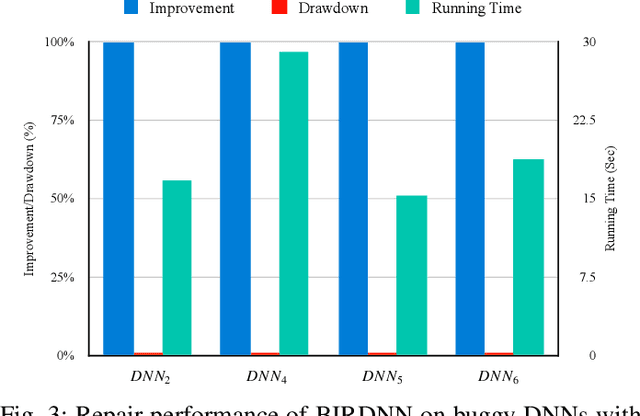
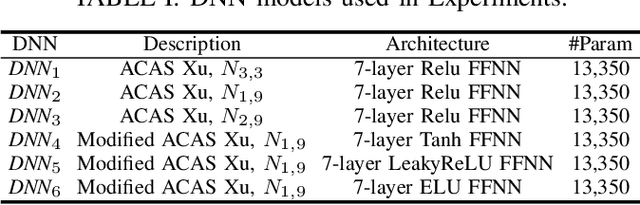
The increasing use of deep neural networks (DNNs) in safety-critical systems has raised concerns about their potential for exhibiting ill-behaviors. While DNN verification and testing provide post hoc conclusions regarding unexpected behaviors, they do not prevent the erroneous behaviors from occurring. To address this issue, DNN repair/patch aims to eliminate unexpected predictions generated by defective DNNs. Two typical DNN repair paradigms are retraining and fine-tuning. However, existing methods focus on the high-level abstract interpretation or inference of state spaces, ignoring the underlying neurons' outputs. This renders patch processes computationally prohibitive and limited to piecewise linear (PWL) activation functions to great extent. To address these shortcomings, we propose a behavior-imitation based repair framework, BIRDNN, which integrates the two repair paradigms for the first time. BIRDNN corrects incorrect predictions of negative samples by imitating the closest expected behaviors of positive samples during the retraining repair procedure. For the fine-tuning repair process, BIRDNN analyzes the behavior differences of neurons on positive and negative samples to identify the most responsible neurons for the erroneous behaviors. To tackle more challenging domain-wise repair problems (DRPs), we synthesize BIRDNN with a domain behavior characterization technique to repair buggy DNNs in a probably approximated correct style. We also implement a prototype tool based on BIRDNN and evaluate it on ACAS Xu DNNs. Our experimental results show that BIRDNN can successfully repair buggy DNNs with significantly higher efficiency than state-of-the-art repair tools. Additionally, BIRDNN is highly compatible with different activation functions.

Credit Assignment for Trained Neural Networks Based on Koopman Operator Theory

Credit assignment problem of neural networks refers to evaluating the credit of each network component to the final outputs. For an untrained neural network, approaches to tackling it have made great contributions to parameter update and model revolution during the training phase. This problem on trained neural networks receives rare attention, nevertheless, it plays an increasingly important role in neural network patch, specification and verification. Based on Koopman operator theory, this paper presents an alternative perspective of linear dynamics on dealing with the credit assignment problem for trained neural networks. Regarding a neural network as the composition of sub-dynamics series, we utilize step-delay embedding to capture snapshots of each component, characterizing the established mapping as exactly as possible. To circumvent the dimension-difference problem encountered during the embedding, a composition and decomposition of an auxiliary linear layer, termed minimal linear dimension alignment, is carefully designed with rigorous formal guarantee. Afterwards, each component is approximated by a Koopman operator and we derive the Jacobian matrix and its corresponding determinant, similar to backward propagation. Then, we can define a metric with algebraic interpretability for the credit assignment of each network component. Moreover, experiments conducted on typical neural networks demonstrate the effectiveness of the proposed method.

Safety Verification for Neural Networks Based on Set-boundary Analysis

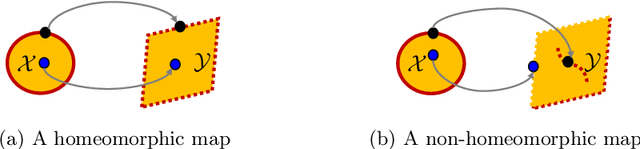
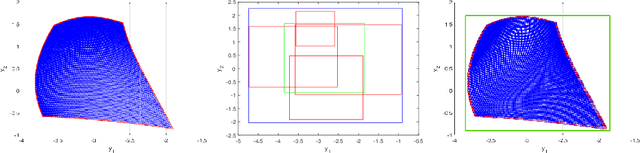
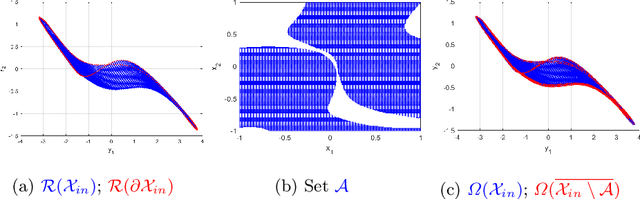
Neural networks (NNs) are increasingly applied in safety-critical systems such as autonomous vehicles. However, they are fragile and are often ill-behaved. Consequently, their behaviors should undergo rigorous guarantees before deployment in practice. In this paper we propose a set-boundary reachability method to investigate the safety verification problem of NNs from a topological perspective. Given an NN with an input set and a safe set, the safety verification problem is to determine whether all outputs of the NN resulting from the input set fall within the safe set. In our method, the homeomorphism property of NNs is mainly exploited, which establishes a relationship mapping boundaries to boundaries. The exploitation of this property facilitates reachability computations via extracting subsets of the input set rather than the entire input set, thus controlling the wrapping effect in reachability analysis and facilitating the reduction of computation burdens for safety verification. The homeomorphism property exists in some widely used NNs such as invertible NNs. Notable representations are invertible residual networks (i-ResNets) and Neural ordinary differential equations (Neural ODEs). For these NNs, our set-boundary reachability method only needs to perform reachability analysis on the boundary of the input set. For NNs which do not feature this property with respect to the input set, we explore subsets of the input set for establishing the local homeomorphism property, and then abandon these subsets for reachability computations. Finally, some examples demonstrate the performance of the proposed method.

Ensemble Defense with Data Diversity: Weak Correlation Implies Strong Robustness

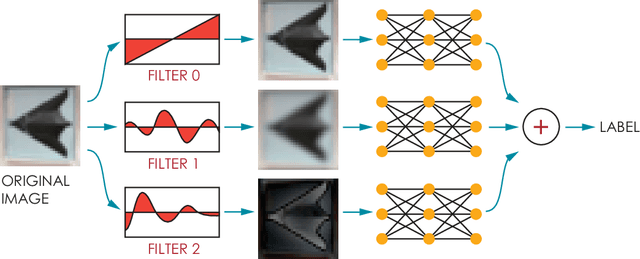
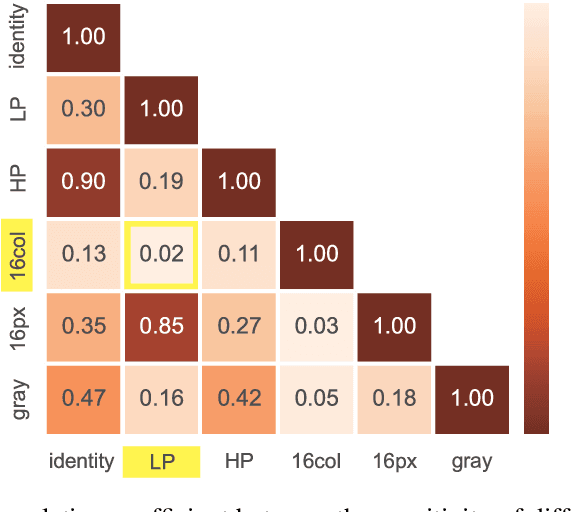
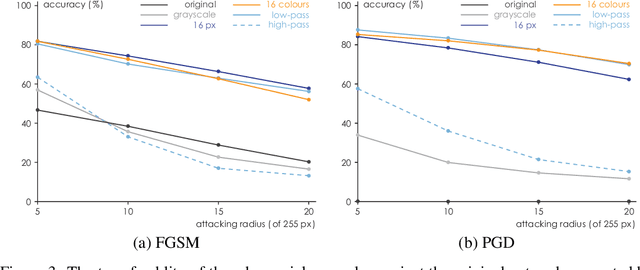
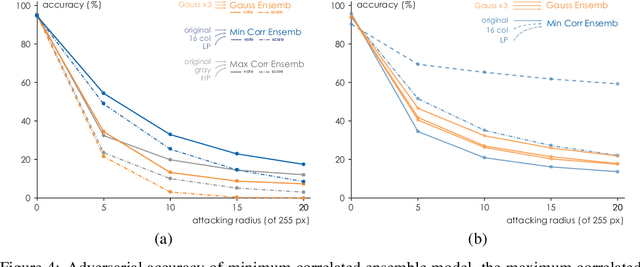
In this paper, we propose a framework of filter-based ensemble of deep neuralnetworks (DNNs) to defend against adversarial attacks. The framework builds an ensemble of sub-models -- DNNs with differentiated preprocessing filters. From the theoretical perspective of DNN robustness, we argue that under the assumption of high quality of the filters, the weaker the correlations of the sensitivity of the filters are, the more robust the ensemble model tends to be, and this is corroborated by the experiments of transfer-based attacks. Correspondingly, we propose a principle that chooses the specific filters with smaller Pearson correlation coefficients, which ensures the diversity of the inputs received by DNNs, as well as the effectiveness of the entire framework against attacks. Our ensemble models are more robust than those constructed by previous defense methods like adversarial training, and even competitive with the classical ensemble of adversarial trained DNNs under adversarial attacks when the attacking radius is large.

Probabilistic Robustness Analysis for DNNs based on PAC Learning

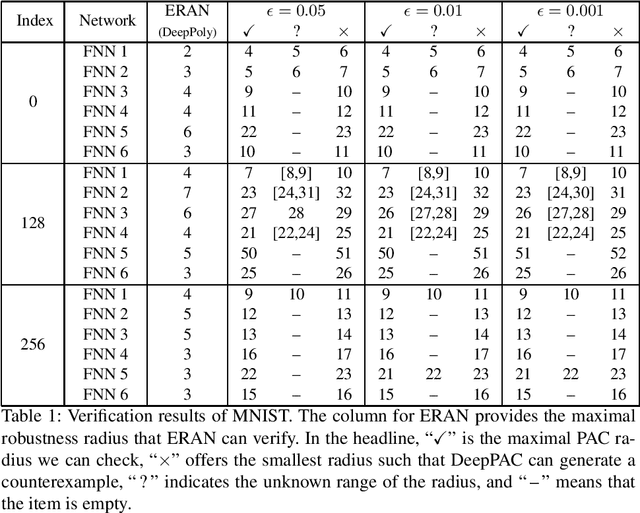
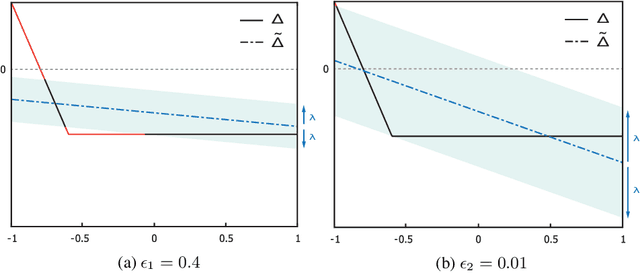
This paper proposes a black box based approach for analysing deep neural networks (DNNs). We view a DNN as a function $\boldsymbol{f}$ from inputs to outputs, and consider the local robustness property for a given input. Based on scenario optimization technique in robust control design, we learn the score difference function $f_i-f_\ell$ with respect to the target label $\ell$ and attacking label $i$. We use a linear template over the input pixels, and learn the corresponding coefficients of the score difference function, based on a reduction to a linear programming (LP) problems. To make it scalable, we propose optimizations including components based learning and focused learning. The learned function offers a probably approximately correct (PAC) guarantee for the robustness property. Since the score difference function is an approximation of the local behaviour of the DNN, it can be used to generate potential adversarial examples, and the original network can be used to check whether they are spurious or not. Finally, we focus on the input pixels with large absolute coefficients, and use them to explain the attacking scenario. We have implemented our approach in a prototypical tool DeepPAC. Our experimental results show that our framework can handle very large neural networks like ResNet152 with $6.5$M neurons, and often generates adversarial examples which are very close to the decision boundary.

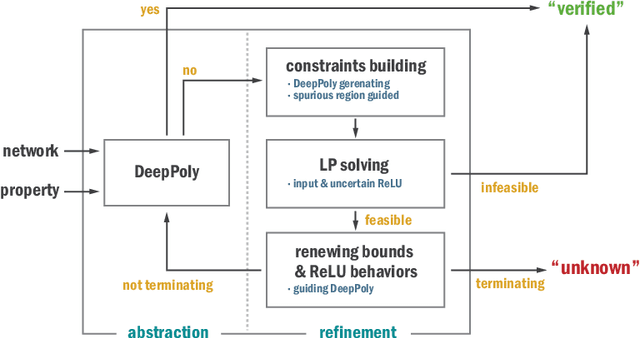
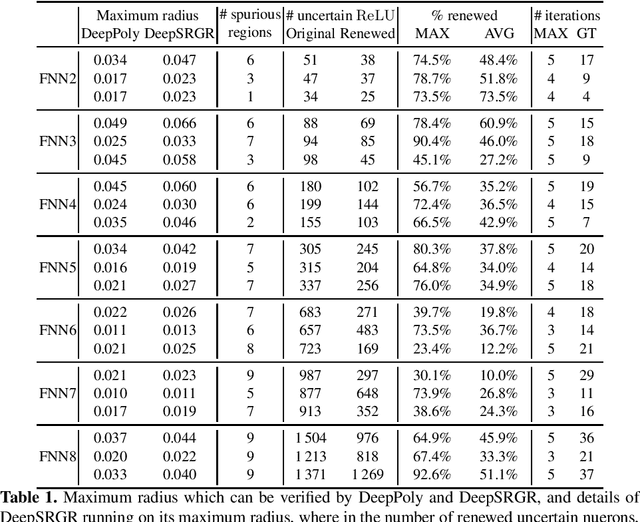
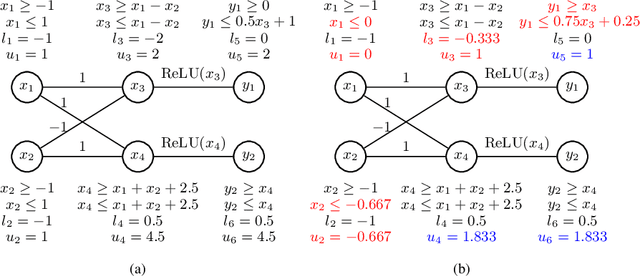
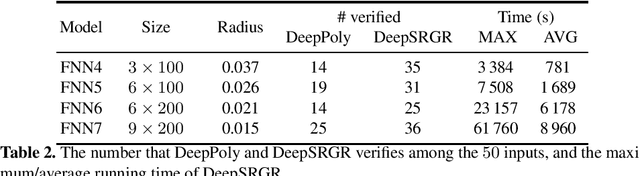
Improving Neural Network Verification through Spurious Region Guided Refinement

We propose a spurious region guided refinement approach for robustness verification of deep neural networks. Our method starts with applying the DeepPoly abstract domain to analyze the network. If the robustness property cannot be verified, the result is inconclusive. Due to the over-approximation, the computed region in the abstraction may be spurious in the sense that it does not contain any true counterexample. Our goal is to identify such spurious regions and use them to guide the abstraction refinement. The core idea is to make use of the obtained constraints of the abstraction to infer new bounds for the neurons. This is achieved by linear programming techniques. With the new bounds, we iteratively apply DeepPoly, aiming to eliminate spurious regions. We have implemented our approach in a prototypical tool DeepSRGR. Experimental results show that a large amount of regions can be identified as spurious, and as a result, the precision of DeepPoly can be significantly improved. As a side contribution, we show that our approach can be applied to verify quantitative robustness properties.

PAC Model Checking of Black-Box Continuous-Time Dynamical Systems

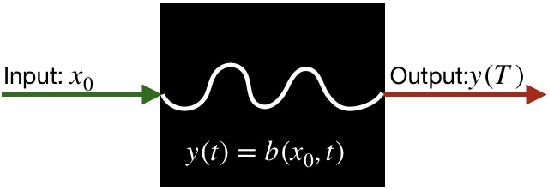
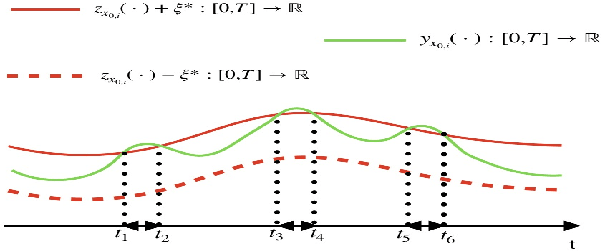
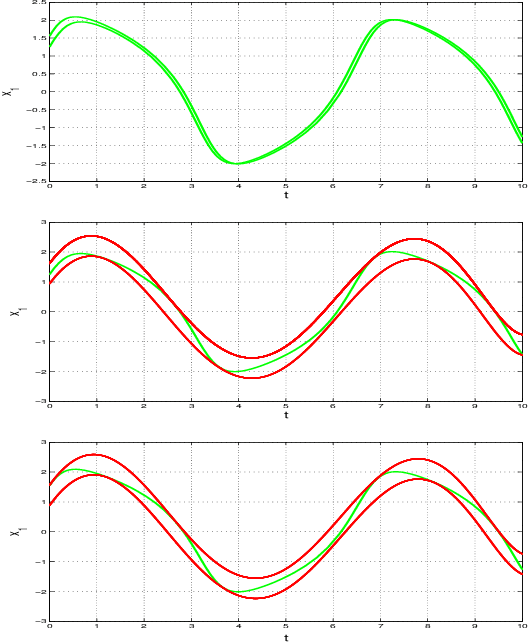
In this paper we present a novel model checking approach to finite-time safety verification of black-box continuous-time dynamical systems within the framework of probably approximately correct (PAC) learning. The black-box dynamical systems are the ones, for which no model is given but whose states changing continuously through time within a finite time interval can be observed at some discrete time instants for a given input. The new model checking approach is termed as PAC model checking due to incorporation of learned models with correctness guarantees expressed using the terms error probability and confidence. Based on the error probability and confidence level, our approach provides statistically formal guarantees that the time-evolving trajectories of the black-box dynamical system over finite time horizons fall within the range of the learned model plus a bounded interval, contributing to insights on the reachability of the black-box system and thus on the satisfiability of its safety requirements. The learned model together with the bounded interval is obtained by scenario optimization, which boils down to a linear programming problem. Three examples demonstrate the performance of our approach.