On Sufficient and Necessary Conditions in Bounded CTL
Paper and Code
Mar 13, 2020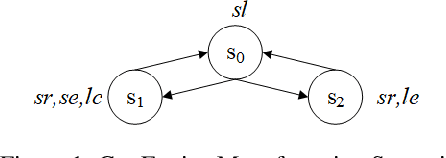
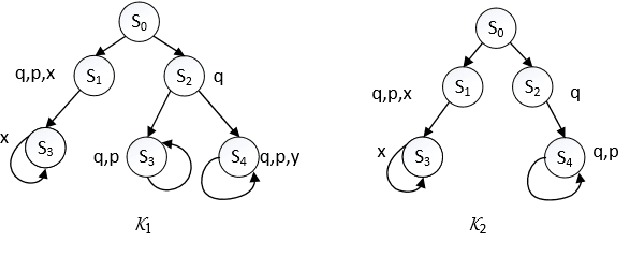

Computation Tree Logic (CTL) is one of the central formalisms in formal verification. As a specification language, it is used to express a property that the system at hand is expected to satisfy. From both the verification and the system design points of view, some information content of such property might become irrelevant for the system due to various reasons e.g., it might become obsolete by time, or perhaps infeasible due to practical difficulties. Then, the problem arises on how to subtract such piece of information without altering the relevant system behaviour or violating the existing specifications. Moreover, in such a scenario, two crucial notions are informative: the strongest necessary condition (SNC) and the weakest sufficient condition (WSC) of a given property. To address such a scenario in a principled way, we introduce a forgetting-based approach in CTL and show that it can be used to compute SNC and WSC of a property under a given model. We study its theoretical properties and also show that our notion of forgetting satisfies existing essential postulates. Furthermore, we analyse the computational complexity of basic tasks, including various results for the relevant fragment CTLAF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge